

「数学の計算革命(駿台受験シリーズ)」<改訂版>
| ページ | 誤 | 正 |
|---|---|---|
| p.121 6行目 | \(6xy-3x+3y-2=9-2\) | \(6xy-4x+3y-2=9-2\) |
| p.271 下から2行目 | \(\int \sin^{4}x \cos x =\) | \(\int \sin^{4}x \cos x\, dx =\) |
「大学受験生のための教科書 新数学Plus Elite数学I・A(駿台受験シリーズ)」
| ページ | 誤 | 正 |
|---|---|---|
| p.5 2行目 | 絶対記号 | 絶対値記号 |
| p.24 解答(4)の右 解説2行目 |
\(x^{4}+1\) は実数係数の範囲では… | \(x^{4}+1\) は有理係数の範囲では… |
| p.24 脚注10 | どんな多項式も… | 定数以外のどんな多項式も… |
| p.45 下から2行目 | \(0x > 3\) | \(0x > 5\) |
| p.76 図 (対偶を示す右下の囲み) |
\(\overline{p} \Rightarrow \overline{q}\) | \(\overline{q} \Rightarrow \overline{p}\) |
| p.80 章末問題 第8問(2) 2行目 |
\(\frac{\sqrt{2}+\sqrt{10}}{a-\sqrt{5}}\) の小数部分をy | \(\frac{\sqrt{2}+\sqrt{10}}{\sqrt{a-\sqrt{5}}}\) の小数部分をy |
| p.86 6行目 | \(Y\) 軸方向に | \(y\) 軸方向に |
| p.167 1行目 | \(\cos \theta= -\frac{\sqrt{3}}{2}\) | \(\cos x= -\frac{\sqrt{3}}{2}\) |
| p.170 (304) (1),(2) | \(\sin \alpha\) \(\cos \alpha\) |
\(\sin a\) \(\cos a\) |
| p.179 11行目 | (\(k=2R\) とおいた) | 該当箇所不要のため削除 |
| p.199 1,3,11行目, 表内 p.199 3行目 |
階級値 データの階級値 |
データの数値 |
| p.226 5行目 | \(a\sigma(X)\) | \(|a|\sigma(X)\) |
| p.540 17行目 p.540 19行目 |
右辺に \(c \neq 0\) を追加して… \(a = b \iff \) … |
両辺に \(c \neq 0\) を追加して… (\(a = b\) かつ \(c \neq 0\)) \(\iff\) … |
| p.584 正三角形の図 | 辺BCの長さ 8 | 辺BCの長さ 15 |
| p.587 脚注5 | \(\mathbb{Z}(\sqrt{-5})\) | \(\mathbb{Z}[\sqrt{-5}\,]\) |
| 解答編 p.2 下から 3行目 |
\(n\) を整数として | \(n\) を正の整数として |
| 解答編 p.65 下から 8行目 |
\(y=x\) のとき最小になるから… | \(y=3\) のとき最小になるから… |
「大学受験生のための教科書 新数学Plus Elite数学II・B(駿台受験シリーズ)」
| ページ | 誤 | 正 |
|---|---|---|
| p.32 9行目 | 複素数 \(a+bi\) は \(b=0\) のときは \(a\) となり、これは実数である。 | 複素数 \(a+bi\) は \(b=0\) のときは実数 \(a\) と定義する。 |
| p.79 7行目 | \(n=k+1\) | \(m=k+1\) |
| p.80 11行目 | \(\alpha^{2^{m}}=x_{1}x_{2}\cdots\cdots x_{n}\alpha^{2^{m}-n}\) | \(\alpha^{2^{m}}\geqq x_{1}x_{2}\cdots\cdots x_{n}\alpha^{2^{m}-n}\) |
| p.81 7行目 | より (**) は成り立つ。 | より (**) は成り立つ。等号は \(x_{1}=x_{2}\) のとき成り立つ。 |
| p.81 23行目 | (**) は成り立つ。 | (**) は成り立つ。等号は、\(x=\alpha\) かつ \(n=k\) の場合の等号成立条件より \(x_{1}=x_{2}=\cdots =x_{k}\) のとき成立するから、\(x_{1}=x_{2}=\cdots =x_{k}=x_{k+1}\) のとき成立する。 |
| p.136 脚注12 | これに垂直な \(l_{2}\) の傾きは 0 であるが、それは、\(b_{1}=0\) のとき \(a_{1}\neq 0\) となるので、\(a_{1}a_{2}+b_{1}b_{2}=0\) より \(a_{2}=0\) が得られる。 | \(l_{1}\) と \(l_{2}\) が垂直であれば \(l_{2}\) の傾きが 0 だから、\(a_{2} =0\) なので、\(a_{1} a_{2}+b_{1} b_{2}=0\) である。\(b_{1}=0\) のとき、\(a_{1} \neq 0\) なので、\(a_{1} a_{2} +b_{1} b_{2} =0\) であれば、\(a_{2} =0\) が得られるから、\(l_{1} \perp l_{2}\) が得られる。 |
| p.253 8行目 | ことによって得られる。 | ことによって得られる。 ただし、(i) の「2 式から \(t\) を消去する」ことで得られる式が \(y=F(x)\) あるいは \(x=G(y)\) の形 (\(F(x), G(y)\) はそれぞれ \(x, y\) の関数) で表されるものとする。 |
| p.312 下から3行目 | \(\theta =\frac{\pi}{2} \pi\), … | \(\theta =\frac{\pi}{2}\) , … |
| p.353 解答1行目右 解説3行目 |
\(\cos □=\frac{\sqrt{2}}{2}\) … | \(\cos □=\frac{\sqrt{3}}{2}\) … |
| p.376 脚注6 | $$\lim_{x\rightarrow 0}b_{n}=\beta$$ | $$\lim_{n\rightarrow 0}b_{n}=\beta$$ |
| p.433 下から2行目 | $$\lim_{x\rightarrow\infty}f(x)g(x)=\infty$$ | $$\lim_{x\rightarrow a}f(x)g(x)=\infty$$ |
| p.448 13行目 | \(x\rightarrow 0\) のとき… | \(h\rightarrow 0\) のとき… |
| p.494 18行目 | ような条件考えるとよい. | ような条件を考えるとよい. |
| p.566 グラフ内 | このとき面積は最大になる. | このとき面積は最小になる. |
| p.904 10行目 | \(P(X=k, Y=l)=\) \(P(X=k)P(Y=l)\) |
\(P(X=x_{k}, Y=y_{l})=\) \(P(X=x_{k})P(Y=y_{l})\) |
| p.955 6行目 | (2) 信頼区間… | (2) 信頼度95%の信頼区間… |
| p.956 4行目 | 母比率 \(\overline{p}\) を … | 母比率 \(p\) を … |
| 解答編 p.231 8行目 |
満たす \(b\) は存在するが … | 満たす \(p\) は存在するが … |
| 解答編 p.298 11行目 |
\(\gt 4\cdot 6k^{2}-6k^{2}-6k-2\) | \(\geqq 4\cdot 6k^{2}-6k^{2}-6k-2\) |
| 解答編 p.298 11行目右解説 |
\(k^{3}=k\cdot k^{2}\gt 6k^{2}\) | \(k^{3}=k\cdot k^{2}\geqq 6k^{2}\) |
「大学受験生のための教科書 新数学Plus Elite数学III(駿台受験シリーズ)」
| ページ | 誤 | 正 |
|---|---|---|
| p.v 16行目 | 本来間違って使い方 … | 本来間違った使い方 … |
| p.32 脚注2行目 | \(b\) は 0 以外の実数 | \(b\) は 0 を含む実数 |
| p.62 脚注 | アメリカの数学者 | イギリスの数学者 |
| p.161 下から1行目 | \(y=\pm \frac{b}{a}\) | \(y=\pm \frac{b}{a}x\) |
| p.190 下から3行目 | \(a, b\) の条件は | \(p, q\) の条件は |
| p.279 下から6行目 | \(x^{2}\geqq x+2\) | \(x^{2}=x+2\) |
| p.314 6行目 | 無限等比級数 | 無限級数 |
| p.315 下から2行目~p.316 4行目 | PDFファイルをご参照ください | |
| p.337 2行目 | \(x=a\) を含むある区間で, つねに |
\(x=a\) を含むある区間で, \(x=a\) 以外で, つねに |
| p.388 下から2~1行目 | \(I=[a,b]\) とおく ... \(I\) で連続で, \((a,b)\) で微分可能である |
\(J=[x_{1}, x_{2}]\) とおく ... \(J\) で連続で, \((x_{1},x_{2})\) で微分可能である |
| p.439 4行目 | \(S=\int^{2\pi}_{0}y\, dx\) (\(\leftarrow x:0 \to 2\pi\) ... |
\(S=\int^{2\pi r}_{0}y\, dx\) (\(\leftarrow x:0 \to 2\pi r\) ... |
| p.521 11行目 | \(I\) は次のようになる | \(J\) は次のようになる |
| p.551 5行目 | \(f(x)\) は \(a\leqq x \leqq b\) で定義 されているものとする. |
\(f(x)\) は \(a\leqq x \leqq b\) で定義 され連続であるものとする. |
| p.553 10行目 | \(|\Delta_{i}|=0\) | \(|\Delta_{i}|\rightarrow 0\) |
| p.566 5、15行目 | \(k=1,2,3,\cdots n\) | \(k=0,1,2,\cdots n\) |
| p.721 最後の行 | 分子が小さい方 … | 分母が小さい方 … |
| p.735 6行目 | \(A_{12}=\{1,5,6,11\}\) | \(A_{12}=\{1,5,7,11\}\) |
| p.743 12行目 | 一番多いのは … | 一番大きいのは … |
| p.855 図 | \(dx=-3dx\) | \(dy=-3dx\) |
| 解答編 p.24 3行目 |
\(y=\frac{\sqrt{2}}{9}x^{2}\) | \(y=\frac{1}{2\sqrt{2}}x^{2}\) |
| 解答編 p.238 4行目 |
1 | \(\frac{\pi}{2}\) |
| 解答編 p.276 6行目右解説 |
\(\left[\frac{1}{2}x^{3}\right]^{t}_{1}\) | \(\left[\frac{1}{2}x^{2}\right]^{t}_{1}\) |
「計算のエチュード 計算の基礎・知識編」 電子書籍版
※ 電子書籍版のみの訂正です。また、最新版のデータ(管理番号:A007f)ではすでに修正されているものもあります。訂正前のデータをご購入済の方は、Amazon に申請することで最新のデータに更新することができます。
| ページ | 誤 | 正 |
|---|---|---|
| p.5 1行目 | 解答が練習問題のすぐにあります。 | 解答が練習問題のすぐ後にあります。 |
| p.13 4 行目 | \(\alpha=\cos \frac{2\pi}{11}\pi+i\sin\frac{2\pi}{11}\) | \(\alpha=\cos \frac{2\pi}{11}+i\sin\frac{2\pi}{11}\) |
| p.47 3行目 | 線型接合 | 線型結合 |
| p.50, 51 (107) (1) | \(k\) | \(n\) |
| p.51 下から3行目 | 分母が定数ではないので, 分母が定数になるように |
分子が定数ではないので, 分子が定数になるように |
| p.57 4 行目 | \(\frac{x^{2}}{2e^{x^{2}}(e^{2x^{2}}-1)}\) | \(\frac{2x^{2}}{2e^{x^{2}}(e^{2x^{2}}-1)}\) |
| p.74 9 行目 | \(\alpha=\cos \frac{2\pi}{11}\pi+i\sin\frac{2\pi}{11}\) | \(\alpha=\cos \frac{2\pi}{11}+i\sin\frac{2\pi}{11}\) |
| p.84 10 行目 | \(\frac{8}{5}+\textstyle\sum\limits_{k=1}^{\infty}\left(\frac{3}{5}\right)^{n+1}\) | \(\frac{8}{5}+\textstyle\sum\limits_{n=1}^{\infty}\left(\frac{3}{5}\right)^{n+1}\) |
| p.100 2 行目 | (3) \( (x,y,z)=\left(\frac{1}{\sqrt{7}},\frac{2}{\sqrt{7}},\frac{4}{\sqrt{7}}\right)\) | |
| p.111 18 行目 | 少なくなありません | 少なくありません |
| p.114 7 行目 | \(x \pm 3\) | \(x =\pm 3\) |
| p.137 13行目 | \(x^{2}-2x+3\) | \(x^{2}-2kx+3\) |
| p.144 14, 18 行目 | ② | ① |
| p.151 3 行目 | ③ かつ ② ⇒ ③ かつ ① | ③ かつ ① ⇒ ③ かつ ② |
| p.151 4 行目 | ② | ① |
| p.156 7 行目 | \( x^{y}\) | \( x^{2}\) |
| p.158 答の数値 | (3) \( (x,y,z)=\left(\frac{1}{\sqrt{7}},\frac{2}{\sqrt{7}},\frac{4}{\sqrt{7}}\right)\) | |
| p.177 16 行目 | \(x\geqq 0\) | \(-x\geqq 0\) |
| p.187 欄外解説2行目 | このようなしなければ | このようにしなければ |
| p.188 9 行目 | \( (2\cos 3x -1)(\cos 3x -1)\) | \( (2\cos 3x -1)(\cos 3x -1)=0\) |
| p.214 17行目 | 最大値は \(\frac{1}{2}e^{-\frac{\sqrt{3}}{6}\pi}\), 最小値は\(-\frac{1}{2}e^{-\frac{7\sqrt{3}}{6}\pi}\) |
\(-\frac{1}{2}e^{-\frac{7\sqrt{3}}{6}\pi}\leqq f(x) \leqq \frac{1}{2}e^{-\frac{\sqrt{3}}{6}\pi}\) |
「計算のエチュード 計算の基礎・知識編」
| ページ | 誤 | 正 |
|---|---|---|
| p.13 4 行目 p.53 9 行目 |
\(\alpha=\cos \frac{2\pi}{11}\pi+i\sin\frac{2\pi}{11}\) | \(\alpha=\cos \frac{2\pi}{11}+i\sin\frac{2\pi}{11}\) |
| p.59 10 行目 | \(\frac{8}{5}+\textstyle\sum\limits_{k=1}^{\infty}\left(\frac{3}{5}\right)^{n+1}\) | \(\frac{8}{5}+\textstyle\sum\limits_{n=1}^{\infty}\left(\frac{3}{5}\right)^{n+1}\) |
| p.81 18 行目 | 少なくなありません | 少なくありません |
| p.97 13行目 | \(x^{2}-2x+3\) | \(x^{2}-2kx+3\) |
| p.126 欄外解説2行目 | このようなしなければ | このようにしなければ |
| p.147 右段 17 行目 | 線型接合 | 線型結合 |
| p.148 右段 18, 19行目 |
分母が定数ではないので, 分母が定数になるように |
分子が定数ではないので, 分子が定数になるように |
| p.174 右段 12, 13行目 |
最大値は \(\frac{1}{2}e^{-\frac{\sqrt{3}}{6}\pi}\), 最小値は\(-\frac{1}{2}e^{-\frac{7\sqrt{3}}{6}\pi}\) |
\(-\frac{1}{2}e^{-\frac{7\sqrt{3}}{6}\pi}\leqq f(x) \leqq \frac{1}{2}e^{-\frac{\sqrt{3}}{6}\pi}\) |
「計算のエチュード 計算の基礎・知識編[数学 I, II, A, B 用]」 電子書籍版
| ページ | 誤 | 正 |
|---|---|---|
| p.73 17 行目 | 少なくなありません | 少なくありません |
「計算のエチュード 計算の基礎・知識編[数学 I, II, A, B 用]」
| ページ | 誤 | 正 |
|---|---|---|
| p.58 17 行目 | 少なくなありません | 少なくありません |
「計算のエチュード 戦略編」 電子書籍版
| ページ | 誤 | 正 |
|---|---|---|
| p.219 1行目 | \(x=0,\frac{\pi}{2}\) | \(x=0,\frac{\pi}{4},\frac{\pi}{2}\) |
「計算のエチュード 戦略編」 ペーパーバック版
| ページ | 誤 | 正 |
|---|---|---|
| p.220 左段 24行目 |
\(x=0,\frac{\pi}{2}\) | \(x=0,\frac{\pi}{4},\frac{\pi}{2}\) |
「計算のエチュード 戦略編(2022年度版)」 電子書籍版
| ページ | 誤 | 正 |
|---|---|---|
| p.13 下から 2 行目 | 三角形 ABC | 三角形 OAB |
| p.60 7 行目 | \(\textstyle\sum\limits_{k=0}^{2n}na_{k}=a_{0}+\cdots\) | \(\textstyle\sum\limits_{k=0}^{2n}a_{k}=a_{0}+\cdots\) |
| p.63 8 行目、17 行目 | ABC の面積 | OAB の面積 |
| p.65 4 行目 | \(\triangle\) ABC | 三角形 OAB |
| p.165 3 行目 | \(x^{3}+\frac{16}{x}\) | \(x^{2}+\frac{16}{x}\) |
| p.219 1行目 | \(x=0,\frac{\pi}{2}\) | \(x=0,\frac{\pi}{4},\frac{\pi}{2}\) |
「計算のエチュード 戦略編(2022年度版)」 ペーパーバック版
| ページ | 誤 | 正 |
|---|---|---|
| p.13 下から 2 行目 | 三角形 ABC | 三角形 OAB |
| p.39 7 行目 | \(\textstyle\sum\limits_{k=0}^{2n}na_{k}=a_{0}+\cdots\) | \(\textstyle\sum\limits_{k=0}^{2n}a_{k}=a_{0}+\cdots\) |
| p.40 8 行目、17 行目 | ABC の面積 | OAB の面積 |
| p.42 4 行目 | \(\triangle\) ABC | 三角形 OAB |
| p.107 3 行目 | \(x^{3}+\frac{16}{x}\) | \(x^{2}+\frac{16}{x}\) |
| p.216 左段 24行目 |
\(x=0,\frac{\pi}{2}\) | \(x=0,\frac{\pi}{4},\frac{\pi}{2}\) |
「数学の受験教科書 1 数と式」
| ページ | 誤 | 正 |
|---|---|---|
| p.86 4行目 |
指す範囲は範囲はっきり | 指す範囲ははっきり |
「数学の受験教科書 2 関数」
| ページ | 誤 | 正 |
|---|---|---|
| p.106 11行目 | (\(k=2R\) とおいた) | 該当箇所不要のため削除 |
「数学の受験教科書 5 ベクトル」
| ページ | 誤 | 正 |
|---|---|---|
| p.17 図 | 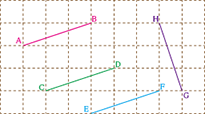 |
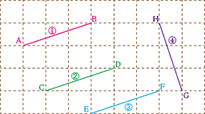 |
| p.36 3行目 | \(r\sin\alpha +s\sin(\alpha +\beta)\) \(-t\sin(\alpha +\beta -\gamma)\) |
\(r\sin\alpha +s\sin(\alpha +\beta)\) \(+t\sin(\alpha +\beta -\gamma)\) |





