数学教育研究所スタッフです。

センター試験・数学、前日のfm yokohama「Future Scape」出演に合わせて清が作成した「センター試験の秘訣」です。
オリジナルデータはpdfですので、ダウンロードの上、明日のセンター試験に是非役立てて下さい。

清史弘オリジナル（2011.01.15）「センター試験の秘訣.pdf」をダウンロードする

下記は、pdfのオリジナルデータからテキストデータと数式部分を画像で記したものです。

センター試験の注意事項

1 　センター試験ってどこが特殊なの?

センター試験ほど多くの受験生が受ける試験はない。したがって, センター試験には数学がかなり苦手な人から相当に得意な人までが受験する。このような幅広い層が一同に受けるが, センター試験はこの多くの受験者の得点を学力別に分布させなければならない。つまり, 数学の苦手な人達の中から, 全く苦手な人, やや苦手な人の得点に差が現れるように作らなければならない。

さて, それでは作る側の立場に立つとどのように問題を作成するとよいだろうか。それは, とりあえずやさしい問題から難しい問題までを並べることであり, このようにして問題は作られる。ここで, やさしい問題は必ず設問の最初の方に配置される。

例えば, 数学I ・数学A の2 次関数の問題であれば, 最初は2 次式を平方完成してグラフの頂点の座標を求める問題, 三角比であれば, 最初は正弦定理あるいは余弦定理を使う問題といったように, 出題される問題までがほぼ決まっている。どの大問もこのように最初はやさしいので, 最初の問題で安心してしまうと, 問題の最後の面倒な問題が待っていて, (設問の前半のペースで解いていると) 時間がなくなるので注意しよう。

また, センター試験は問題の中で使われる知識, 定理によって問題が構成される。例えば, 三角比であれば正弦定理あるいは余弦定理を知っているかを問う問題は必ず含まれなければならない。したがって, 正弦定理あるいは余弦定理を使う状況になるようにわざわざ問題が作られ, これが国公立の2 次試験の問題の作り方と決定的に違う点である。このようにして作られた問題は設問間の関連が弱いことが多く, 必ずしも小問の(1) で得られたことが(2) で活かせるわけではない. むしろ(1) と(2) は別々の問題のことが多々あるので, 小問ごとに問題を最初から解くような感じであり, これらの問題を解くのに意外と時間がかかる。作業もある程度早く処理できることが要求される。

2 　ありがちなマークミス

マークミスをあまくみていてはいけない。自分は大丈夫と思っていても万が一マークする位置が1 つずつずれたりなどすると致命傷になってしまう。「そんなことはしないよ」と思うかもしれないが, 案外多いのは次のようなミスである。

のように, アとイを2 回ずつ使って出題することがある。しかし, うっかりすると, 最初の例のようにア～エまでの記号を使っているものの思いこみ,ア2 　イ3 　ウ2 　エ3をマークしてしまう。

実際, 2009 年数学II・数学B 第1 問[2] では,

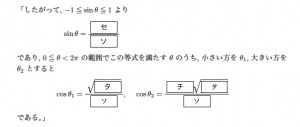
とあるが, ソとタは2 回ずつ使われているのでマークの際は注意しなければならない。

3 　設問ごとの特徴

• 各大問の序盤から難しいことを問われることはまずない
もしも, 大問の最初の方の問題で悩んだ場合は, 「最初から難しい問題は出ることはないはず」と考えて, 何か簡単なことを忘れていないだろうかと考えてみよう。

• 2 次関数の問題は頂点の座標を中心に考えよう。
センター試験の数学I・A の問題で「2 次関数のグラフがx 軸に接する」と言えば, 「グラフの頂点のy 座標が0」と考えるとよい。また, グラフの移動については, 頂点がどこにうつるかを考えよう。

• 数学I・A の第3 問の図形の問題
まず, 落ち着いて正確な図を描いてみよう。正確な図を描くことで図の特徴に気がつくことはよくあることである。
また, 「円に内接する四角形とあれば向かい合う角の和が180◦」のように定番のものはすぐに使えるようにすることは大切。
三角比の問題として出題されることの多い第3 問であるが, 平面図形の知識(方べきの定理・メネラウスの定理など) も警戒が必要。

• 確率の問題で最後に期待値を求める問題
最後に期待値を求める問題は, 結局のところ確率変数の取りうる値すべての確率を求めなければならない。その場合, 一番求めにくい確率は確率の総和1 から引く方式で求めるように問題の流れが作ってあるのがセンター試験の通例である。

例えば, 昨年の問題のように確率変数X が0, 1, 2 を取り, その期待値を求める場合, 結局はX = 0, 1, 2 となる確率を求めなければならないが, 一番求めにくいX = 2 となる確率は1 からX = 0, 1 となる確率を引く方法で求めるように問題が仕組まれている。

• 2005 年以前の数列の過去問はあまり参考にならない。
旧課程では数列は数学A の中にあった(今は数学B)。数学A の問題として数列が出ていたころは, 等差数列, 等比数列が中心で特に数列をグループごとに分けた群数列の問題が多い。しかし, 現行課程になって数学B の問題として出題されるようになってからは, 等差数列, 等比数列の問題は出題されるものの新たに漸化式の問題が多く出題されるようになり, 問題自体も難しくなっている。

したがって, 問題集で古い過去問を使っている場合は, 少し傾向が異なるから注意が必要である。

• ベクトルの問題は時間がかかる
数学B の問題として出題されるベクトルの問題は結構時間がかかるものが多いので, 時間配分に注意しよう。

• 雑でもよいから
あまり勧めたいことではないが, やはりセンター試験の場合は雑でもよいから早く答を出した者が評価される試験である。

例えば, 数学II の問題で

数学II の微分の問題で増減表は書かなくてもお咎めなしであるなど, 間違えない程度に雑でもかまわない。センター試験が終わったら, 丁寧な答案を書くように心がけよう。

センター試験の試験中に何か迷ったら, とりあえず先に進むのが得策です。ひとつの問題にあまり時間をかけないようにしましょう。また, 「マークをあとでまとめて」と考えている人は時間配分に注意しましょう。マークするだけで3 ～ 5 分くらいかかります。