

プラスエリートに関する意見・質問
- 数学の内容に関する意見・質問
- Q51.
- p1000 円と放物線が接する条件について 某問題集では、(類題で)まず図を描き、二点で接するか、一点で接するかを場合分けをして解いており、二点で接する場合に重解条件を用いていました。円と放物線が接する問題において、重解条件を用いても正解となる問題がありますが、それは偶然と捉えるべきでしょうか。円と放物線が接する問題で重解条件を使っても良い裏付けにはどのような場合が考えられますか。全く整理がつかないです。(2021.5.4)
- A51.
- まず、事実として、放物線の頂点以外で円と接する場合は、重解条件をうまく使えば求めることはできます。しかし、それには理由があり(本来の接する条件と一致することの証明など)、そこを無視して「正しければいいんだ」というスタンスと「理由を無視した丸暗記的なものはだめだ」というスタンスがあります。本書は後者ですが、どちらをとるかは教える側の責任と考え方があるので、一律に考え方が違うものを否定するわけにはいかないと思います。
繰り返しになりますが、重解条件を用いて正解が得られる場合は理由がありますので、それを「偶然」と呼ぶかどうかの判断は難しいと思います。
裏付けは、先ほども述べたように、2曲線が接する条件から変形していきます。 - Q52.
- p.253 の【軌跡の求め方1】 この記述が誤りとのことですが、どのように直せば成文になるのでしょうか。(2021.5.7)
- A52.
- 申し訳ございません。その記述がある部分ではそこで取り上げられているような簡潔な多項式関数 (\(x, y\) の少なくとも一方が \(t\) の1次式、あるいは \(x\) に対して \(y\) が一つに決まる場合) しか想定していませんでしたが、一般の \(f(t), g(t)\) にまで広げるとそれぞれの値域だけでは求めることが出来ません。読者は当然その方法を一般の場合に適用しようと考えるでしょうからこのままでは誤りとなります。
そして、その後の学習も考えた場合、この方法は、その後の注でも触れていますが、\(x^{2}+y^{2}=1\) のように「\(y=u(x)\) あるいは \(x=v(y)\) (\(u(x), v(y)\) はそれぞれ \(x, y\) の関数) のように、\(x\) に対し \(y\) が一つしか決まらない関数の形で表せないもの」に対しては「\(x\) の値域を調べても不十分」(もちろん \(y\) の値域を調べても不十分、両方調べても不十分) であると書いたつもり (つまりこの方法は適用できない) でしたが、この注は枠内に入れるべきだったと思います。(当然、そこしか読まないケースもでてきてしまいますので)
その後で学習するケースとしては、例えば、\(x=\cos t, y=\sin t\) で \(t\) のとり得る範囲が \(0\leqq t\leqq \frac{3}{2} \pi\) の場合などが (これは \(y=u(x)\) の形にならない) あり、\(x\) の値域、\(y\) の値域の両方を調べても正しい結果はわかりません。そのような場合は特殊な場合を除き、パラメータの存在条件に頼ることになります。
結局のところ、枠内の文言は注で指摘しているつぎの文章が足りていません。
(i) の「2式から \(t\) を消去する」ことで得られる式が \(y=F(x)\) あるいは \(x=G(y)\) の形 (\(F(x), G(y)\) はそれぞれ \(x, y\) の関数) で表されるものとする。
このような場合ならば、適用できます。なお、ここでは、\(t\) の取り得る範囲が「区間」であることにも注意してください。
今後はこれを枠内に入れることとします。 - Q53.
- p725の「ベクトルは向きと大きさをもった量である」とは2、3次元ベクトル空間での定義ですか?p1040の内容を学ぶと4次元以上のベクトル空間での向きや大きさの定義がよくわかりませんでした。高校数学でのベクトルの定義は幾何ベクトルに限定しているのでしょうか?(2021.5.21)
- A53.
- 「向きと大きさをもった量」というのは、最初の幾何ベクトルの導入によく用いられる表現なので、ベクトルの学習の入り口として使いました。微分係数が、学習初歩で「接線の傾き」として、説明されるのと同じです。
4 次元以上のベクトルになると、「向き」「大きさ」は、定義しなければなりませんので、そこまでの範囲を指して書いているわけではありません。そのくらいになると、ベクトルとはベクトル空間の元として定義します。 - Q54.
- p281の下から7行目の「(?)または(?)はもっと簡単に『α+β>0またはαβ<0』と表すこともできる」というのがわかりません。なぜαβ≧0を省けるのでしょうか。お願いします。(2021.5.26)
- A54.
- (i), (ii) から「\(\alpha +\beta \gt 0\) または \(\alpha\beta\lt 0\)」は自明です。逆に「\(\alpha +\beta\gt 0\) または \(\alpha\beta\lt 0\)」がいえる場合を考えましょう。
・\(\alpha +\beta\gt 0\) がいえる場合、\(\alpha\) と \(\beta\) が異符号でなければ \(\alpha\beta\geqq 0\) が言えます。\(\alpha\) と \(\beta\) が異符号ならば \(\alpha\beta\lt 0\) がいえます。
すなわち、\(\alpha +\beta\gt 0\) の場合は、「\(\alpha +\beta \gt 0\) かつ \(\alpha\beta\geqq 0\)」か「\(\alpha\beta\lt 0\)」のいずれかが成り立ちます。
・\(\alpha\beta\lt 0\) の場合は (ii) が成り立ちます。
したがって、「\(\alpha +\beta\gt 0\) または \(\alpha\beta\lt 0\)」の場合は (i), (ii) の少なくとも一方がいえることになります。 - Q55.
- |a?+a?+・・・+an|≦|a?|+|a?|+・・・+|an|のような不等式を証明したいとき方針としてプラスエリート2b、70ページの三角不等式の証明をn回繰り返すといった認識で良いのでしょうか?注意点などあれば教えてください。(2021.5.27)
- A55.
- はい。その考え方でよいです。数学的帰納法のように、n 個の文字で成立しているときに、n+1 個にしても成り立つことを示しておけばよいですね。
- Q56.
- p273の問題について。このようにαとβが実数になる条件を考えなければならないと気づくポイントなどはありますか。条件反射的にα+βとαβとα^2 +β^2<1などの不等式がある時に考えるようにしています。このような和と積であればαとβは不等式を満たす共役複素数として存在できると考えておく程度で良いでしょうか。ご教授いただけると幸いです。(2021.5.31)
- A56.
- 例えば、\(X=x+2y, Y=2x-y\) のように \(X,Y\) が \(x,y\) の 1 次式で表されている場合は、\(X,Y\) が実数の場合、\(x,y\) も実数になるので、いわゆる「元の変数が実数で存在するか」を気にしなくても正しい答は得られますが、\(X=x+y, Y=xy\) の「\(Y=xy\)」のように 2 次式(あるいはそれ以上)になると、\(X,Y\) が実数でも \(x,y\) が実数であるとは限らなくなるので、\(x,y\) が「実数で存在する」ことを調べなければなりません。
ですので、\(X,Y\) が \(x,y\) のどのような式で表されるかに注目することが大切です。 - Q57.
- p32に「複素数a+biはb=0のときはaになり…」とあるのですが、この、0×i=0というのは、定義ですか?定理ですか?一見当たり前と思える複素数の和、差、積はきちんと定義してあるのに対し、0×i=0は当たり前としていいのか、疑問に思ってしまいました。(2021.6.1)
- Q58.
- Q57の者です。p33の積の定義にのっとり0×iを考えるためには、そもそも0をa+biの形で表すことが必要になります。しかし0に対応する(a,b)の値がa=0、b=0とできるのは、0+0×i=0となること、すなわち0×i=0を前提として用いなければなりません。だとすると、この定理「0×i=0」は、複素数の積の定義から導出する際、自分自身「0×i=0」を用いてしまっていることになりませんか?(2021.6.4)
- A57., A58.
- 非常に重要なご指摘です。結論は定理ではなく、定義という立場です。少し詳しく説明しましょう。
以下、\(a,b\) 等の文字は実数とします。\(a+bi\) に用いられる「\(+\)」は普段、実数の加法に用いられている「\(+\)」とは異なりますので、ここでは、あえて \(a+bi\) を \(\lt a,b\gt\) のように 2 つの実数のペアとして表記することにします。
p.33 にある、複素数の加法 \(\lt a,b\gt +\lt c,d\gt =\lt a+c,b+d\gt\)、複素数の乗法 \(\lt a,b\gt\times\lt c,d\gt=\lt ac-bd,ad+bc\gt\) は新しい複素数という数体の定義ですが、ここに入る前に、次のようなものを定義する必要がありました。
複素数の相当 \(\lt a,b\gt =\lt c,d\gt\) であるとは \(a=c\) かつ \(b=d\) であること
複素数体の実数体への埋め込み \(\lt a,0\gt =a\) つまり、\(\lt a,0\gt\) という 2 つの数の組が \(a\) という実数と同等にみなせるようにした。これは、ベクトル \((a,0)\) を実数 \(a\) とみなすようなもので(ベクトルの場合はそうしません)、本来カテゴリーの違うものを結び付ける役目があります。\(\lt a,0\gt =a\) の特別な場合が、\(\lt 0,0\gt =0\) ですが、これを定義しておかなければ先に進めないのでした。
そこで、p.32 の「複素数 \(a+bi\) は \(b=0\) のときは \(a\) となり、これは実数である。」は「複素数 \(a+bi\) は \(b=0\) のときは実数 \(a\) と定義する。」のような表現に訂正します。
なお、\(\lt a,0\gt =a\) については、演算の定義の後で定義(というより埋め込み)してもかまいませんが、どちらにしても、\(\lt a,0\gt =a\) と演算の定義が無矛盾であることの証明は必要になります。
(Q57. と Q58. の回答は統合いたしました。) - Q59.
- Q57,58の者です。何度もすみません。これまでの話はよくわかったのですが、そうなるとさらに疑問に思ってしまう点があります。それは、p36例題1-11(1)のような証明問題は、定義そのものだから、もはや問題として成立していないのでは?ということです。もしくは、複素数の相等が定義されていなければ、問題文にある条件「a+bi=0」がそもそも考えようがないのでは?ということです。ただ、ほかの参考書や数学学習者向けのウェブサイトにも、「複素数の相等の証明」が結構載っています。これらもすべて、定義だから成り立って当たり前、で済んでしまうということですか?それとも当初のA57にあった通り、立場によって定義と定理が異なるため、それぞれの立場によって問題として成立したり、成立しなかったりするということですか?数学の世界でそんなことが起こりえるのでしょうか。大混乱ですみません。大パニックと言ってもいいです。またさらに、たとえば中学校ではじめて無理数を扱い始めたときなども、数字を拡張するときには、たとえば√2×0=0などは、当たり前と考えると実は危険なのでしょうか?(2021.6.8)
- A59.
- プラスエリート IIB の「初版」をお持ちでしょうか。その部分については、同様の指摘もあり、第 2 版以降では、
「\(a+bi=0\)」ではなく、「\(a+b\alpha =0\)」(\(\alpha\) は虚数) になっているはずです。
ご指摘の通り、\(a+bi=0\) の場合は定義そのものではないか、だから、証明はおかしいという意見を頂きました。一方でそのままでもよいと言われる方もいたのですが、やはりこの本では \(a+bi=0\) であることの定義という立場をとり変更しました。
数学の世界では、定義の仕方が異なることはよくあることです。例えば、自然対数の底 \(e\) の定義も様々です。どれでなければならないということもありません。
ですので、「定義は何か?」という設問だけだと愚問であることもあり、大切なのは、一度決めた定義からその周辺の定理の関係を理解することにあります。 - Q60.
- さて、P.831問8-20について質問があります。ベクトルOA自体がxz平面と垂直では無いため、xz平面に平行で、ベクトルOAに垂直な直線は存在しないように思えてなりません。手で平面を作ってあれこれ動かしてみましたがやはり納得いかず…。自分の考えがなぜ誤っているのか、ご指摘いただけましたら幸いです。初歩的な質問になり大変恐縮ですが、よろしくお願いいたします。(2021.6.11)
- A60.
- そのような場合は、答から考えてみるとよいと思います。解答にある直線の方向ベクトルは (1,0,-1) ですが、これは y 成分が 0 なので xz 平面に平行です。また、ベクトル (2,1,2) との内積も 0 ですから、ベクトル OA とも垂直です。ベクトル OA が xz 平面と垂直でないから直線が一つに定まります。逆に OA が xz 平面と垂直であれば、求める直線は無数に存在します。
- Q61.
- P596の例の計算がなぜ書いているようになるのか理解できません。(2021.7.7)
- A61.
- まず最初に与えられているのは、数列 \(a_{n}\) の 1 番目から \(n\) 番目までの和の値です。
求めたいのは、10 番目~20 番目までの和です。
ですので、
(10 番目~20 番目までの和) = (1 番目から 20 番目までの和) – (1 番目から 9 番目までの和)
となります。つまり 1 番目から 20 番目までの和を求めると、余分な 1 番目から 9 番目の和が入って来てしまいますのでこれを除きます。
1 番目からの和にこだわるのは、もちろん与えられた条件が 1 番目からの和になっているからです。 - Q62.
- p221の補足の(2.20)の不等式はどのように導きますか。私は、絶対値のついた文字を右辺に移項して、もう一方の文字の絶対値を外して考えましたが、この方法は合っていますか。また、(2.20)の不等式は入試の記述解答に用いても良いでしょうか。ご多忙の中恐縮ですがよろしくお願いします。(2021.7.12)
- A62.
- \(|Y|\leqq a-|X|\) として、\(-(a-|X|)\leqq Y\leqq a-|X|\) のように変形します。次にこれを
\(|X|\leqq a+Y\) かつ \(|X|\leqq a-Y\)
として、それぞれを
\(-(a+Y)\leqq X\leqq (a+Y)\) かつ \(–(a-Y)\leqq X\leqq a-Y\)
とすれば、
\(-a\leqq X+Y\leqq a\) かつ \(-a\leqq X-Y\leqq a\)
が得られます。
記述解答の件ですが、問題次第ですが、ここが中心の問題でなければかまわないとは思います。ですが、いつも同じ返答ですが、入試の採点を決めるのは大学側ですので、絶対にこうだのようなことは言えません。 - Q63.
- P598に、等差数列の定義は、n+1項目-n項目が定数dとなることである、とある一方、注には、等差数列の一般項はnの一次式になる、とあります。これはd=0の場合に矛盾が生じます。d=0の場合は等差数列と言いますか?言わないですか?(2021.7.16)
- A63.
- \(d=0\) の場合は、非常に特殊で、その数列は等差数列でもあり、等比数列でもあります。
正確な表現としては、「\(d\) が 0 でないとき、等差数列は \(n\) の 1 次式になる」とすべきでした。 - Q64.
- P604の等差数列の例題7-2の解答で余りによる分類をしていますが、なぜ6kではなく6k+6で分類しているのでしょうか?書いてある内容は理解できるのですが、先に余りによる分類とことわっておいてから6k+6と書くと、余りの条件(ここでは0≦r≦5)を満たしていないような気がして、果たしてこれは余りによる分類なのかと疑問に思ってしまいました。(2021.7.22)
- A64.
- \(6k+6\) としているのは、その前の段階で \(k=0,1,2,\cdots\) のように 0 を含めているからです。\(6k\) にするとこの場合だけ、\(k\) は 1 以上になります。
- Q65.
- プラスエリート2Bの初版(第三版)なのですが、p365(三角関数の節末問題)の解答編p125の解答で、f(x)の最大値最小値を求めるのにg(t)の最大値最小値で答えてしまっても大丈夫なのでしょうか?(2021.7.25)
- A65.
- \(f(x)\) を途中で \(g(t)\) に置き換えているだけですから、\(g(t)\) の最大値、最小値がそのまま \(f(x)\) の最大値、最小値になるので問題はありません。
より、詳しく説明するのなら、\(f(x)\) の最大値、最小値は \(g(t)\) の最大値、最小値に等しい、などと書いておけばよいと思います。 - Q66.
- p.858,の内容についての質問です。一般に、→a=→b ならば →a?→c=→b?→c の逆は成り立たないと思うのですがp.858 八行目で→nとの内積をとって元のベクトル方程式と同値な平面の方程式が得られたのは何故なのでしょうか?→x_0 の終点が表したい平面内にあるという仮定が効いてるのでしょうか?それとも、単に→x_0,→u,→v が一次独立だからなのでしょうか?というよりそもそも(8.17)と(8.18)は同値ではないのでしょうか?あるいは他に何か理由があるのでしょうか?(2021.7.27)
- A66.
- \(\vec{x}=\vec{x_{0}}\) ならば \(\vec{n}\cdot\vec{x}=\vec{n}\cdot\vec{x_{0}}\) ですが、逆はいえません。
(8.17) の付近を言葉を追加して説明してみます。\(\vec{u}\) と \(\vec{v}\) は 1 次独立で、\(\vec{n}\) は \(\vec{u}\) と \(\vec{v}\) の両方に垂直な \(\vec{0}\) でないベクトルとします。
\(({\rm A}) \vec{x}\) は \(\vec{x}=\vec{x_{0}}+s\vec{u}+t\vec{v}\) (\(s,t\) はある確定した実数)
\(({\rm A}') \vec{x}\) は \(\vec{x}=\vec{x_{0}}+s\vec{u}+t\vec{v}\) を満たす実数 \(s,t\) が存在するようなベクトルである。
\(({\rm B}) \vec{x}\) は \(\vec{n}\cdot\vec{x}=\vec{n}\cdot\vec{x_{0}}\) を満たすベクトルである。
この場合、\(({\rm A})\Rightarrow({\rm B})\) ですが、\(({\rm B})\Rightarrow({\rm A})\) ではありません。
一方、\(({\rm B})\) のとき、すなわち、\(\vec{n}\cdot(\vec{x}-\vec{x_{0}})=0\) のとき、\(\vec{x}-\vec{x_{0}}\) は、ある実数 \(s,t\) を用いて \(\vec{x}-\vec{x_{0}}=s\vec{u}+t\vec{v}\) と表せる (これを認めることとします) ので、\(({\rm B})\Rightarrow({\rm A}')\)、すなわち、\(({\rm A}')\Longleftrightarrow({\rm B})\) が言えます。 - Q67.
- p683の例題7-19の(1)の答は ー2^n +1 +2・5^n/-3 (-2)^n-1 +2 ・5^n でも良いですか?(2021.8.10)
- A67.
- 解答にある答の分母分子に \((-1)^n\) をかけたように見えるのですが、その場合、分子の第 1 項が違いますので、このままでは誤りになります。
- Q68.
- 解答解説の方の298ページの上から10行目の部分の文頭にはなぜ等号が付かないのでしょうか。(2021.8.17)
- A68.
- 失礼しました。これは誤植です。\(k\geqq 6\) ですので、等号が入ります。右の欄外の説明の部分も同様に入ります。
- Q69.
- 解答解説の方の326ページの3行目の式のようになるのはなぜですか。(2021.8.25)
- A69.
- その前の式である p.325 の下から2行目の式 ① をうけての立式になります。P が平面 BCD にあることから 3 つのベクトル AB, AC, AD の係数の和が 1 であることを利用しています。
- Q70.
- 879ページの例題8-37についての質問です。θが90度よりも大きくなる場合も考慮してといているようにおもうのですが、θが90度を超えるのは具体的にはどのような場合でしょうか。(2021.8.31)
- A70.
- θは 90゜を超えません。 ベクトル AP とベクトル AB のなす角は90゜を超えることはあります。
- Q71.
- 解答解説の方の347ページの大門7についての質問です。-?√?3→a・→bの大きさが?√?3となっていますが大きさとかんがえずに そのまま プラス・マイナス?√?3としても良いですか。(2021.9.6)
- A71.
- 文字化けが一部ありますが、解答の (1) の 4 行目の式についてとして答えます。
\(|-\sqrt{3} \vec{a}\cdot\vec{b} |=\sqrt{3}\)
の中の \(-\sqrt{3}\vec{a}\cdot\vec{b}\) はスカラー、すなわちここでは実数値ですので、この式から
\(-\sqrt{3} \vec{a}\cdot\vec{b} =\pm\sqrt{3}\)
とするのはかまいません。 - Q72.
- p614の部分分数分解型の和を求める際に例えば(1)ならn=1とn≧2、(2)ならn=1,2とn≧3で場合分けして解かなくてもよいのでしょうか?(2021.9.7)
- A72.
- 厳密にいえば、しないよりはした方がよいとは思いますが、この程度は許されるかと思います。もちろん、許さないという人もいると思いますので場合分けをする方が安全です。
例えば、\(1+2+\cdots +n=\frac{1}{2} n(n+1)\) も普通は \(n=1\) と \(n\geqq 2\) で場合分けしないと思います。 - Q73.
- (ただの感想です) 元駿台3号館の生徒です。先生には数学zsを習っていました。当時は私の実力不足で数学xsの問題で分からない所がたくさんあり、それが大学進学後もずっと心残りでした。そこで今回プラスエリートの?B、?を自分用に購入しました。この本にはまるで宝石を散りばめたような、素晴らしい解説が随所に見られました。学習参考書とは思えない、数学書のように真摯な態度で書いてある文章に心を打たれました。私が特に気に入ったのはコーシーシュワルツの不等式と、不等式の同値変形の部分です。駿台を卒業して時間が経ってしまいましたがプラスエリートを何回も読み返しながら当時習得出来なかった箇所を復習したいです。先生もお体に気をつけて下さい。これからも応援しています。(2021.10.21)
- A73.
- 丁寧なご感想をありがとうございます。今後もさらによい本になるように努めていきたいと思います。
- Q74.
- 階差数列で質問なのですが a(n+1)=a1+(階差数列の1からnまでの和) としてn≧2を考慮せず計算してはいけないのでしょうか?(2021.11.1)
- A74.
- その場合も \(a_{n+1}\) で求めて、\(a_{n}\) に戻す段階で \(n\geqq 2\) の制限が必要になります。
例えば、「\(a_{n+1}=(n+1)^{2}\) \((n=1,2,3,\cdots )\)」
から、「\(a_{n} =n^{2}\) \((n=1,2,3,\cdots )\)」とすることはできず、「\(a_{n} =n^{2}\) \((n=2,3,4,\cdots)\)」となります。 - Q75.
- Q74のものです。回答ありがとうございました。また別の疑問なんですが、普通に漸化式を解く際、a_(n+1)+f(n+1)=~ の次の行にはa_n+f(n)=~の形にできるのは何故でしょうか?例えば、階差数列型とは違い、p667(1)の解答5行目の「したがって」以降に突然a_nとしてよいのは何故でしょうか?(2021.11.1)
- A75.
- まず、\(a_{n+1}+f(n+1)\) を変形して \(a_{n}+f(n)\) になったわけではありません。この 2 式の \(n\) は別の \(n\) です。
漸化式では、 「\(n+1\) 番目は \(n\) 番目を使ってこのように書ける」ということを主張し、
「それだったら、一般の \(m\) 番目(漸化式の \(n\) と無関係) は初項を使ってこう書ける」
と主張しているのが後者の式です。この \(m\) を慣例に従い \(n\) のままで表しているということになります。 - Q76.
- P52の二次方程式の解と係数との関係の証明の際に因数定理を用いていますが、二次方程式の解が重解の場合も因数定理で証明できるのでしょうか?二次方程式f(x)=0の重解をaとして、因数定理を用いてf(x)は(x-a)^2で割り切れるといえるのでしょうか?(2021.11.28)
- A76.
- この質問に答えるにあたって、「そもそも重解とは何か」から始まります。
そもそも、「解」と「根」は異なるものです。「解」自体は、方程式を満たすものですから、2次方程式に限らず、指数方程式、あるいは微分方程式などにもあります。一方、「根」は正確には「多項式の根」です。重解は本来は重根です。重根と考えれば、因数定理を経由せずに、\(f(x)=a(x-\alpha )^{2}\) が定義そのものです。そのような考え方ももちろんよいです。
さて、\(\alpha\) と \(\beta\) が異なるとき、\(\alpha\)、\(\beta\) が 2 次方程式 \(f(x)=0\) の解であるとは、\(f(\alpha )=0, f(\beta )=0\) の両方が成り立つことを意味します。
これは、
\(f(\alpha )=0\) であるから、\(f(x)=(x-\alpha )Q(x)\) と表せる。(因数定理より)
そして、\(f(\beta )=0\) であるから、\(Q(\beta )=0\) より \(Q(x)=(x-\beta )\times (定数)\) と表せる
ことより、\(f(x)=a(x-\alpha )(x-\beta )\) と表せます。
\(\alpha\) を \(f(x)=0\) の重「解」と考えた場合、この延長で、(\(\beta\) を \(\alpha\) と考えることにすると)
\(f(\alpha )=0\) であるから、\(f(x)=(x-\alpha )Q(x)\) と表せる。
そして、「\(\alpha\) が重解」を「商がもう一度 \(\alpha\) を解にもつ」(先ほどの \(\beta\) を \(\alpha\) と見る)と考えれば \(Q(x)=(x-\alpha )\times (定数)\)と表せる
ことから、\(f(x)=a(x-\alpha)^{2}\) の形になると考えられます。
このような解釈なら因数定理を使ったことになります。ですが、そもそも、(重根でなく) 重解という言葉自体があいまいですのでこのようになってしまいます。 - Q77.
- p.904 確率変数の独立の部分にて、X=k,Y=lの部分はX=x_k,Y=y_lの間違いでしょうか。(2022.1.30)
- A77.
- 誤植のご連絡ありがとうございます。ご指摘の通りですので、訂正させていただきます。
- Q78.
- p831の問い8-20について 具体的な答案が載っておらず、自分の答案に不安があるのですが、想定解をご教授頂けますでしょうか?(2022.5.13)
- A78.
- この問いの説明については、解説動画を作りましたので、以下のリンク先を見てください。
問い8-20解説動画 - Q79.
- いつも清先生の著書やTwitterの投稿を参考させていただいて数学の指導をしている者です。新数学 Plus Elite 数学IIB について質問させていただきたく、ご連絡致しました。p280とp281の解答についての質問です。?の2解をαとβとするとき、αβ<0ならば判別式D>0が成り立つことから【1】?が実数解をもつ【2】(i)α+β>0かつαβ≧0 または (ii)αβ<0 という2つの条件は、【1】?が実数解をもつ かつ α+β>0かつαβ≧0 【2】αβ<0 となると思うのです。解答の結果には影響はありませんが、気になりましたので質問させていただきました。(2022.5.18)
- A79.
- もちろん \(\alpha\beta\lt 0\) のときは必ず \(D\gt 0\) になるので、\(\alpha\beta\lt 0\) の場合は、\(D\gt 0\) を気にしなくてもよいです。
そこの解答では、「まず、実数解をもって、その中で解と係数の関係でどう解決できるか」という方針なので、その中で後者で自動的に実数解をもつ場合もあってもおかしいわけではなく、このような場合分けは他にもあります。解決する条件を互いに排反な条件にしなければならないことはありません。
「となると思う」とありますが、それは、好みの問題なので、お好きな方を選択すればよいと思います。 - Q80.
- X,Y:確率変数 この時、積XYも確率変数の証明を教えてください。(2022.6.28)
- A80.
- プラスエリートのどの記述に対しての質問でしょうか。
- Q81.
- 節末問題103について 次の別解は正解としてよいでしょうか。十分性を満たしているのか不安なのですが。f(x)=(x^2+x+1)g(x)+x+2 …(1) f(x)=(x^2+1)h(x)+1 …(2) f(x)=(x^2+x+1)(x^2+1)j(x)+px^3+qx^2+rx+s …(3) とする。(2)でf(i)=1,(3)でf(i)=(-p+r)i+(-q+s)より(-p+r)i-q+s=1複素数の相等により-p+r=0 …(4) -q+s=1 …(5) また、a=(-1+√3i)/2とすると,aはx^2+x+1=0の解の一つであり,またx^3-1=(x-1)(x^2+x+1)より,aはx^3=1の解の一つでもある。これらよりa^2=-a-1=(-1-√3i)/2a^3=1とa^3=1が言える。(1)でf(a)=a+2=√3/2+√3/2i (3)でf(a)=pa^3+qa^2+ra+s=(p-q/2-r/2+s)+(-√3/2q+√3/2r)i だから、複素数の相等により p-q/2-r/2+s=√3/2 …(6) -√3/2q+√3/2r=√3/2 …(7) (4)から(7)よりp=1,q=0,r=1,s=1以上から求める余りはx^3+x+1(2022.8.3)
- A81.
- 因数定理を複素数の範囲で使う部分はかまいません。
複素数の相等を使うのであれば、最初に p,q などが実数であることに触れておいた方がよいでしょう。
余りは一通りに決まることを普通は認め、前提としているので、これでよいと思います。 - Q82.
- p23.例題1-5(1)について質問です。n=kと仮定しn=k+1を示す際に、まずn=kの仮定からf(x)=(xーα1)(xーα2)・・・(xーαk)Q(x)・・・?と言えて、f(αk+1)=0より因数定理からf(x)は因数(xーak+1)をもつ、すなわち、?のQ(x)は(xーak+1)Q2(x) (Q2(x)は多項式)と表され、f(x)=(xーα1)(xーα2)・・・(xーαk)(xーαk+1)Q2(x) この解答に問題があるでしょうか?(2022.12.12)
- A82.
- おおよそよいと思います。
\(\alpha_{k+1}\) は、\(\alpha_{1}, \alpha_{2}, \cdots , \alpha_{k}\) と異なるから、\(Q(α_{k+1})=0\) であるという記述があればさらによいと思います。 - Q83.
- p739:1行目の「Oを座標平面上の原点とする。」そしてその欄外の「一般には原点である必要はなく、基準点と考えると良い。」という記述についてですが、仮にこのOが原点でなかった場合にはある平面上にある点についての座標が分かれば位置ベクトルが分かる、もしくはその逆の関係が成り立たない気がするのですが、どうでしょうか?素人の質問で恐縮ですがよろしくお願いします。(2022.12.18)
- A83.
- このように書いていますが、位置ベクトルは「座標平面上」では原点 O から指すベクトルです。ただし、ここでは、座標平面以外も考え、その場合、位置ベクトルはあらかじめ定めておいて基準点(それを O と呼ぶとは限らない)から指すベクトルと考え、基準点を P と決めていれば P から指すベクトルです。
座標平面上で基準点が原点 O でないことはまずないのではないかと思いますが、それでも O 以外の基準点をとると座標と位置ベクトルの成分は異なり、それを考える意味はほとんどないでしょう。 - Q84.
- p431の図1,2などは例えば数式で表すとしたらどのような感じになるんでしょうか。(2023.1.15)
- A84.
- 図1については、\(f(x)=\displaystyle\lim_{n\to\infty} ([x]-x+1)^{n}\)
図2については、\(f(x)=[x]\)
のようなものがあります。\([ ]\) はガウス記号です。 - Q85.
- p438でのx→2のときx-2分の1→なしというのはx-2分の1という分数関数(まだあまり詳しくやっていませんが)のグラフから理解できるんですけど、p439の0分のc型の極限は+?,-?,存在しないのいずれかになるというのが分かりませんでした。僕の考えとしては例えばx→aのときf(x)が0分のc型になるというのはx=aのときにf(1)が存在しない(分母が0であるから)ってことしか分からないとしか言えないと思ったんですけどどうですか?(2023.1.15)
- A85.
- \(x\to 2\) のときの、\(\frac{1}{x-2}\) の極限が存在しないのは、分数関数 \(\frac{1}{x-2}\) の値が \(x=2\) のときに存在しないからでは「ありません」。
\(x\) が 2 より大きい方から 2 に近づく場合と、2 より小さい方から 2 に近づく場合とでは、\(\frac{1}{x-2}\) が目指している値が異なるので、「存在しない」ということになります。
例えば、\(\frac{1}{x-2}\) の値は、\(x=2.1, 2.01, 2.001,\cdots\) のとき、\(10, 100, 1000,\cdots\) のように限りなく大きくなります。
一方、\(x=1.9, 1.99, 1.999,\cdots\) のときの \(\frac{1}{x-2}\) の値は、\(-10, -100, -1000,\cdots\) のようにどこまでも小さくなります。
これらの目指す先が異なるということで、極限は存在しないということになります。
p.439 の \(\frac{c}{0} (c\neq 0)\) の極限については、簡単な例として、\(\frac{1}{x}, \frac{1}{x^{2}}, -\frac{1}{x^{2}}\) を考えるとよいでしょう。
\(x\) が、\(0.1, 0.01, 0.001,\cdots\) のように 0 に近づくと、
\(\frac{1}{x}\) は、\(10, 100, 1000,\cdots\)
\(\frac{1}{x^{2}}\) は、\(100, 10000, 1000000,\cdots\)
\(-\frac{1}{x^{2}}\) は、\(-100, -10000, -1000000,\cdots\)
となるのに対し、
\(x\) が、\(-0.1, -0.01, -0.001,\cdots\) のように 0 に近づく場合では、
\(\frac{1}{x}\) は、\(-10, -100, -1000,\cdots\)
\(\frac{1}{x^{2}}\) は、\(100, 10000, 1000000,\cdots\)
\(-\frac{1}{x^{2}}\) は、\(-100, -10000, -1000000,\cdots\)
のようになりますが、\(\frac{1}{x}\) は違うところを目指しているので極限は「存在しない」のに対し、\(\frac{1}{x^{2}}\) はどちらも限りなく大きくなるので、極限は \(\infty\)、\(-\frac{1}{x^{2}}\) はどちらも限りなく小さくなるので、極限は \(-\infty\) となります。
これらは、極限が \(\frac{1}{0}\) になる場合のサンプルですが、結論は、「存在しない」「\(\infty\)」「\(-\infty\)」のいずれかです。他の場合で調べてもこの \(\frac{1}{0}\) 型の極限は、この 3 パターンしか現れないということです。 - Q86.
- p549の不定積分の定義について 不定積分である∫[a→x]t dtは ∫[a→x]t dt=1/2x^2-1/2a^2...?ということですが高校での不定積分では∫x dx=1/2x^2+C(Cは任意定数)...?です。?を満たさないCもあるので、?の表記は正確でないと思ってしまいました。でも高校ではCで統一してますよね。Cの条件まで考えなくてよいということでしょうか?(∫[a→ x] f(t)dt+Cを不定積分と定義すれば問題ありませんが...)(2023.2.11)
- A86.
- ご指摘の通りですが、そのことは、p.549 の「あるいは」以降で記してあります。私が昔使っていた古い本には、「\(+C\)」がなく、これは今でも「\(a\) を基点とする不定積分」として、これはこれで不定積分として認められていますが、高校数学で現れる逆微分としての不定積分と整合性をもたせるために、「あるいは」のところで \(+C\) を入れています。「\(+C\)」を入れないと、不定積分は、必ず零点をもってしまい、\(2x\) の不定積分に \(x^{2} +1\) などを含まなくなってしまうからで、このことは、下の注にも書かれています。高校数学であれば、「\(+C\)」の \(C\) は条件をつけず任意定数とする方がよいでしょう。
- Q87.
- p.136の下の注釈に関しての質問です。この注釈は、b1=0のもとでも、「l1とl2が垂直⇔a1a2+b1b2=0」が成り立つことの説明だと思います。しかし個人的には、なぜこの注釈でそれが示せているのか分かりません。自分は最初、単にb1=0のもとで、右向きと左向きをそれぞれ示せばいいと思い、以下のような証明を考えました。「b1=0のもとで、l1とl2が垂直と仮定すると、l1はy軸平行より、l2はx軸平行でa2=0。よって、a1a2+b1b2=0となる。逆に、b1=0のもとで、a1a2+b1b2=0と仮定すると、b1=0よりa1≠0であるから、a2=0。よって、l2はx軸平行となるから、l1とl2は垂直。したがってこれらはb1=0のもとでも同値である。」これを手短に書いたのがこの注釈なのでしょうか?それとも、もっと違う考え方なのでしょうか。お手数ですがご回答頂けるとありがたいです。(2023.2.27)
- A87.
- まず、「~のとき、・・・となる」という書き方は、必要十分な表現ではありません。ここでは、\(b_{1} =0\) のもとでも
\(l_{1} \perp l_{2} \iff a_{1} a_{2} +b_{1} b_{2}=0\)
が成り立つことを言いたかったわけですが、この注釈のスペースでは書ききれず不正確な表現になってしまいました。
ここで書きたかったことは、
\(b_{1}=0\) のもとで、
「\(l_{1}\) と \(l_{2}\) が垂直であれば \(l_{2}\) の傾きが 0 だから、\(a_{2} =0\) なので、\(a_{1} a_{2}+b_{1} b_{2}=0\) である。」
がまず言いたかったことで、次に
「\(b_{1}=0\) のとき、\(a_{1} \neq 0\) なので、\(a_{1} a_{2} +b_{1} b_{2} =0\) であれば、\(a_{2} =0\) が得られるから、\(l_{1} \perp l_{2}\) が得られる」
が、後半で言いたかったことです。
今のままでは、ご指摘の通りよくないので、訂正し、訂正表にも記載しておきます。 - Q88.
- p537の4行目からの式ですが、S=lim n→無限大n分のa-bΣk=1からnまでのf(a+n分のb-ak)のf(xk)の部分であるf(a+n分のb-ak)の公差に当たるb-akがなぜa-bkでないのかが分かりませんでした。(2023.3.1)
- A88.
- 質問の内容がわかりにくいので、適切な回答になっていないかもしれませんが、\(f( )\) の ( ) 内の数列は、\(a\) から始まって \(b\) で終わる数列なので、公差は、\(\frac{b-a}{n}\) になります。図の長さは、\(\frac{a-b}{n}\) になっていますが、これは公差でなく、これが公差になるのは、\(b\) で始まって、\(a\) で終わる数列の場合です。
- Q89.
- p130における0=a(xーx0)+b(yーy0)と0=ax+by+cの方程式の関係についてですが、前者は点x0,y0,を通り、ベクトル(a.b)に垂直な直線を表して、後者は点x0,y0を通るけれどベクトル(a,b)と垂直ではない直線の式を表すかつ、方程式にx0,y0を代入したものを引けば前者の式になる。このような理解で十分でしょうか?(2023.3.18)
- A89.
- p.130 にある \(a(x-x_{0})+b(y-y_{0})=0\) は点 \((x_{0},y_{0})\) を通り、ベクトル \((a,b)\) に垂直な直線です。なので、「前者は・・・」の部分はその理解でよいです。
「後者は・・・」の部分ですが、\(ax+by+c=0\) は結論としてベクトル \((a,b)\) に垂直な直線になります。おそらく、中段の「逆に」以降の質問なのかなと解釈しましたので、そのつもりで説明します。
ここでは、\(ax+by+c=0\) がベクトル \((a,b)\) に垂直であることを証明しようとしています。
そこで、まず、\(ax+by+c=0\) が \((a,b)\) に垂直かどうかわからない段階から始めます。\(ax+by+c=0\) は直線を表すので、その上から点を 1 つとり、それを \((x_{0},y_{0})\) とおきました。この点の取り方は一通りではありませんが、直線上の点ならどこでも同じ結果がいえるのでかまいません。次に、\(ax+by+c=0\) と \(ax_{0} +by_{0} +c=0\) の差をとり、\(a(x-x_{0})+b(y-y_{0})=0\) を作り, これをベクトルの内積と解釈しました。
ここから \((x-x_{0}, y-y_{0})\) が \((a,b)\) と垂直がいえて、\((a,b)\) が直線の法線ベクトルであるといえたということです。 - Q90.
- p725:ベクトルの相等の枠内において、「ベクトルABとベクトルCDは平行移動で重なる」とありますが、ここは平面上の有向線分ABと有向線分CDは平行移動で重ねることができるので、それらが表す(移動量としての)ベクトルは等しい、ということでしょうか。有向線分と幾何ベクトルの違いを気にしているところで本書を参照し、本書はうまく有向線分という言葉を使わずに書かれておりました。そのところで冒頭の表現が出てきたので、これは有向線分のことをベクトルとされているのかが気になりました。(2023.3.27)
- A90.
- 貴重なご指摘をありがとうございます。「有向線分」は、その名の通り向きを持った線分で、その図の有向線分 AB と有向線分 CD は異なる有向線分です。その有向線分の始点から終点までの移動量がベクトルですので、枠内の下の行は、
「有向線分 AB と有向線分 CD が平行移動で重ね合わせることができるとき、それぞれの有向線分がもつベクトル量であるベクトル AB とベクトル CD は等しい (逆も成り立つ)」
あるいは、
「ベクトルAB = ベクトルCD ⇔ 有向線分 AB と有向線分 CD が平行移動で重ねることができる」
ということになります。 - Q91.
- p902確率変数の分散と平均の関係について質問です。途中「ここでX=x_kとなる確率とX^2=(x_k)^2となる確率は等しい」…(*)とありますが、もしx_a=-x_bなるa,b(a≠b、1≦a≦n、1≦b≦n)が存在するときには、(*)は成立しないのではないでしょうか。結果としてΣ(x_k)^2p_k=E(x^2)となること自体はサイコロの例などを考えれば理解できるのですが、途中のこの説明だけしっくりきません。お忙しいとは思いますが回答お待ちしております。(2023.8.16)
- A91.
- まず、「\(X = x_{k}\) となる確率と \(X^{2} = x_{k}^{2}\) となる確率は等しい」は、\(x_{k}\) がすべて正の値をとる場合などの特殊な場合に成立し、一般的には成り立ちません。
具体的な例を出しましょう。簡単のため、確率変数は \(X = −1, 1, 2\) のみをとるとし、それぞれの確率を順に、\(p_{−1}, p_{1}, p_{2}\) とします。\((p_{−1} + p_{1} + p_{2} = 1)\)
このとき確率分布表は次のようになります。
\(X\) \(−1\) \(1\) \(2\) \(P (X)\) \(p_{−1}\) \(p_{1}\) \(p_{2}\)
次に、\(X_{2}\) の確率分布表は次のようになります。
\(X^{2}\) \((−1)^{2}\) \(1^{2}\) \(2^{2}\) \(P (X^{2})\) \((p_{−1})^{2}\) \(p_{1}^{2}\) \(p_{2}^{2}\)
ところが、\((−1)^{2} = 1^{2}\) ですので、これは次のように表せます。
\(X^{2}\) \(1\) \(4\) \(P (X^{2})\) \((p_{−1})^{2}+p_{1}^{2}\) \(p_{2}^{2}\)
したがって、\(P (X = 1^{2}) \neq P (X = 1)\) となり、一般にも \(P (X = x_{k}) \neq P (X^{2} = x_{k}^{2} )\) となります。ただし、その後の \(E(X^{2})\) を求める場合において、
\(E(X^{2}) = (−1)^{2}p_{−1} + 1^{2}p_{1} + 2^{2}p_{2}\)
と計算することは正しい結果が得られ、2 乗する前の元の値で区別して表現する方がわかりやすいと思われます。
結論としては、\(E(X^{2})\) を求める場合に、\(x_{k} = −x_{l}\) となる場合があっても、
\(\displaystyle E(X^{2}) =\sum^{n}_{k=1}(x_{k})^{2}p_{k}\)
のように求めても結果は正しくなります。 - Q92.
- Q52.に対する回答A52.で、その後で学習するケースとしてx=cost, y=sintでtのとり得る範囲が0≦t≦3π/2の場合等はパラメータを消去しxの値域、yの値域の両方を調べても正しい結果は分からない、という旨の記載があります。こちらのケースは「その後で学習するケース」としてプラスエリートシリーズのどこかで解説が記載されておりますか?ご教授いただけると幸いです。またこちらのケースについて、確かにパラメータを消去してもうまくいかずパラメータの存在条件から軌跡を求めようと思ったのですが、論証するとなるとうまく解答が書けず困っております。こちらの解答の方、書籍に記載がないようでしたらご教授いただけると幸いです。どうぞよろしくお願いいたします。(2023.9.5)
- A92.
- p.253 にある「軌跡の求め方1」にある方法は、その下の注意にもあるように、消去した式が特殊な場合に限ります。それにあてはまらない場合は、p.254の「軌跡の求め方2」にある方法に従います。
その問題の場合は
「『\(\displaystyle x=\cos t, y=\sin t, 0\leqq t\leqq \frac{3\pi}{2}\) をすべて満たす \(t\) が存在する (A)』ような \(x,y\) の条件」を求めることが軌跡を求めることにつながります。
その条件の表現にはいくつかの種類がありますが、
「\(x^{2} +y^{2} =1\) かつ \((x\leqq 0\) または \(y\geqq 0)\) (B)」
がそのような \(t\) の存在条件です。
(A) であれば, \(x,y\) は (B) を満たすことと (B) であれば (A) が成り立つことを言えばよいでしょう。 - Q93.
- 解答編315ページ 807についての質問です。この問題のように角度を求める問いの場合、120°と答えるのと2/3πと答えるのとではどちらの方が良いのでしょうか。(2023.9.19)
- A93.
- このような問題の場合、問題文の中にまったく指定がないので、どちらを選ぶかは解答者が決められます。
どちらでも構いません。 - Q94.
- 1の三乗根をオメガと表記することや、その数値の導出については、どこかで解説されていますでしょうか。IIBp.57注13に出てきたり、IIICp.53に突然既知の事柄のように現れたりするのですが、なんのことだったかと迷いが生じてしまっています。どこかに書いてありましたら見つけられておらず、申し訳ございません。(2023.12.31)
- A94.
- ご指摘の通り、p.57 に急に出てきたときには驚かれると思います。本来はそれよりは先に説明すべきことでしたが、そうなっていないので申し訳ございません。1の3乗根は \(x^{3}=1\) を解いて得られます。これは、
\((x-1)(x^{2}+x+1)=0\)
となるので、「原始」3乗根については、\(x^{2}+x+1=0\) を解いた \(\displaystyle \frac{-1\pm\sqrt{3} i}{2}\) のことで、このどちらか、あるいは両方を \(\omega\) を使って表します。 - Q95.
- p906注に、シグマの交換が可能である旨が記載してありますが、その説明の「2つのシグマは独立な和であるから」の意味がよくわかりません。ご説明いただければと思います。(2024.4.23)
- A95.
- 確かにわかりにくい表現だったかもしれません。これは、矢印の指す式の第2項について述べたものです。
矢印の指す式の1つ上の式は、「先に \(l\) についての和をとってから次に \(k\) についての和をとる」ことを表しています。
次に矢印の指している式の第2項では、「先に \(k\) についての和をとってから次に \(l\) についての和をとる」式になっています。
ここでは、このような変形が許されるということを述べました。
実際は、下の画像のような例で納得されるとよいと思います。\(k,l\) の取りうる範囲は、互いに影響されない(これを独立とよんでいる)ので、どちらの和を先に取るかはどちらでもよいということです。
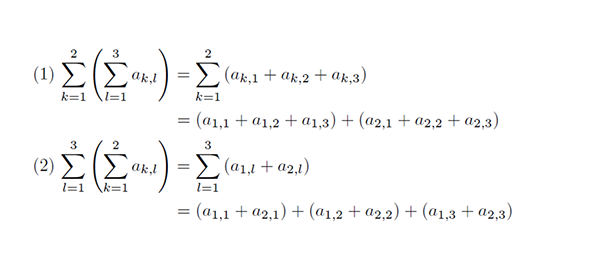
- Q96.(1)
- 不等式の証明に関してお聞きしたいことがあります。P.82例題1-22では、2式とも両辺が正なので辺々かけて・・としていますが P.102節末問題(118)では展開して整理してから相加平均と相乗平均の関係を用いています。この使い分けの判断はどのようにしたら良いでしょうか?(118)は最小値を求める問題であること、a>0,b>0で、a=bかつ3/a=4/bとなるa,bが存在しないこと をはじめに確認して・・・とかでしょうか?例えば自分の持っている問題集で (a+1/b)(b+4/a)≧9を示せ のような問題があり、辺々かけるのではうまくいかず、展開して整理してから・・・となりますが、相加平均と相乗平均の関係で辺々かけても右辺が合わないな・・・と考えて展開、のような考え方で良いのでしょうか?(Q96.(2)へ続く)
- A96.(1)
- まず、p.82 の方ですが、一般には展開して相加平均・相乗平均の関係を使う方が安全です。それは、この関係を「1回しか使わないから」です。2回使うとロスがでることがあります。例えば、\(\sin x\geqq -1, \cos x\geqq -1\) ですが、\(\sin x +\cos x\geqq (-1)+(-1)\) となり、この不等式自体は正しいのですが、実際は、\(\sin x+\cos x\geqq -\sqrt{2}\) であり、もっとよい評価ができます。
別の言い方をしてみます。2つの関数 \(f(x)\) と \(g(x)\) があり、すべての \(x\) に対し \(f(x)\geqq 1, g(x)\geqq 2\) のとき、\(f(x)g(x)\geqq 1×2\) は正しくても \(f(x)g(x)=2\) とならない可能性もあります。それは、\(f(x)=1, g(x)=2\) が同時に成立するとは限らないからです。
「\(f(x)g(x)\) はつねに 2 以上でも、もっと大きい値よりも大きくなる可能性がある」
のです。
p.82 の方は、\(a+b\geqq 2\sqrt{ab}\) の等号が成り立つ \(a,b (a=b)\) と、\(\frac{1}{a} +\frac{1}{b} \geqq \frac{2}{\sqrt{ab}}\) の等号が成り立つ \(a,b (a=b)\) がたまたま同じなのでうまくいきました。うまくいくのならわざわざ展開しないでこれで終わらせたいというのがここの考え方です。
ですが、p.102 (118) の方はその方法では、\(a+b\geqq 2\sqrt{ab}\) の等号が成り立つ場合と \(\frac{3}{a} +\frac{4}{b} \geqq 2\sqrt{\frac{3}{a}\cdot\frac{4}{b}}\) の等号が成立する場合が異なるので、それぞれに相加平均と相乗平均の関係を使うとうまくいかなくなります。特に、(118) の方は「最小値を求めよ」という問題なので、不等式の等号が成り立たなければ必要なことはいえません。
以上の要点をもう一度確認しますと、
・複数個所で相加平均と相乗平均の関係を使うときは、等号が同時になりたつことがあるときに有効。とくに最小値を求める問題では、同時に等号が成り立たないと無意味である。
・一般的に展開して、1か所に相加平均と相乗平均の関係を使う方が安全
ということになります。 - Q96.(2)
- (Q96.(1)の続き)
また、a>b>0,c>d>0ならばac>bdを示せ というような問題でも、条件が両辺ともに正なので辺々かけて・・としても良いでしょうか?解答ではa>bからac>bc、c>dからbc>bd として導いていました。辺々かけて良いのかどうか等をどのように考えて判断しているのかお聞きしたいです。(2024.6.11) - A96.(2)
- 普段は、\(a\gt b\gt 0、c\gt d\gt 0\) のとき \(ac\gt bd\) とするのはかまいません。
ただし、「\(ac\gt bd\) が言えるのはなぜか」と問われれば、それ以前の段階に戻って説明する必要があります。
例えば「6は偶数であるのはなぜか?」と聞かれたときに「6が偶数だから」と答えるのではなく、偶数の定義に戻って、「6は2で割り切れるから」と答えるべきでしょう。しかし、「6は偶数である」は普段はあたりまえのこととしてよいと思います。
ここでは、\(a\gt b, c\gt 0\) のとき \(ac\gt bc\) であるというそこよりも基本的なことを元に説明しているのでしょう。 - Q97.
- p83,86のコーシー・シュワルツの不等式の証明でakが0となるものが存在する場合も比の式であれば成立するとありますが、akが0のものはxkも0で比は0:0となると0:0は全ての比と等しいと考えれば良いのでしょうか?比に0が入る時の考え方を教えて欲しいです。お願いします。(2024.6.28)
- A97.
- \(a:b=x:y\) の定義を \(ay=bx\) と考えるとわかりやすいと思います。\(a=0, b\neq 0\) の場合は、「\(x=0,y\) は任意」です。
\(a=b=0\) の場合は、「\(x,y\) は任意」と考え、実際、それぞれその場合が \((ax+by)^{2} \leqq (a^{2}+b^{2})(x^{2}+y^{2})\) の等号が成り立つ場合です。
\(a:b:c=x:y:z\) の場合も同様に考えるとよいでしょう。 - Q98.
- プラスエリートIIBでは微分の初めのところで「接線の傾きに近づく」という表現をされていますが、IAでもIIBでも接線という言葉は定義されていないように思います。この書き方では微分係数を使わずに定義していると思いますが、どのような定義なのでしょうか。もし、書いてあるページがあればすみません。(2024.7.9)
- A98.
- その章での導入部分での「接線」の定義については、特に定義しておらず図形と式などで曖昧に使われているもの(「円と直線が接する」など)を踏襲しています。
当然のこととして、きちんと定義しておかないと後々困りますが、その本での接線の定義は、曲線 \(y=f(x)\) の \(x=a\) における微分係数 \(f’(a)\) が存在する場合は、直線 \(y=f’(a)(x-a)+f(a)\) です。 - Q99. new
- ベクトルの一次独立を利用した問題について質問です。例題8-11では実数s,tについて範囲を限定せず直線上としていますが、節末問題(805)では線分上として範囲を限定しています。交わる際に線分上であるのが自明であれば範囲を限定する必要は無いが,範囲を限定した方が丁寧であるぐらいの認識で大丈夫ですか?(2024.7.18)
- A99.
- 範囲を指定する方が丁寧でよい説明ではあります。最初にすべての実数の範囲で考えて、結果的に \(0\lt s\lt 1, 0\lt t\lt 1\) になったのでよかったと後で確認する方法もあります。
線分上で交わることが自明な場合は、直線で考えても結果的にはよいので大丈夫ですが、それでもきちんと書くようにした方が安全ではあります。そこにこだわることが重要でない場合には、採点上はスルーされることもあるとは思います。 - Q100. new
- p.838の2直線の距離は正射影によって求まりますが、その時の2直線上の点の座標を求めるには補足のように計算するしかないでしょうか?(2024.7.19)
- A100.
- 2直線上の点の距離が最小になる点の座標を求めるためには、正射影を使う方法の延長では厳しいので、ご指摘の通り補足のような計算になります。
プラスエリートII・B
Q1. ~ Q50.
最新記事
Jul.24 2024
「数学ラウンジ」動画公開のお知らせ
YouTube 数学ラウンジ…
Jul.23 2024
「プラスエリートクラブ」ページ更新のお知らせ
「プラスエリートクラブ」で数…
Jul.21 2024
「数学ラウンジ」動画公開のお知らせ
YouTube 数学ラウンジ…
Jul.19 2024
「数学ラウンジ」動画公開のお知らせ
YouTube 数学ラウンジ…
Jul.19 2024
「プラスエリートクラブ」ページ更新のお知らせ
「プラスエリートクラブ」で数…
Jul.18 2024
「数学ラウンジ」動画公開のお知らせ
YouTube 数学ラウンジ…
Jul.18 2024
「エチュードクラブ」ページ更新のお知らせ
「エチュードクラブ」で計算の…
Jul.17 2024
「数学ラウンジ」動画公開のお知らせ
YouTube 数学ラウンジ…
Jul.11 2024
第13回今後の教育課程、学習指導及び学習評価の在り方に関する有識者検討会について
7月10日に文科省で開催され…
Jul.10 2024
「プラスエリートクラブ」ページ更新のお知らせ
「プラスエリートクラブ」で数…
Jun.29 2024
「プラスエリートクラブ」ページ更新のお知らせ
「プラスエリートクラブ」で数…
Jun.23 2024
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で「3 …
Jun.11 2024
「受験教科書クラブ」「プラスエリートクラブ」ページ更新のお知らせ
「受験教科書クラブ」で「1 …
May.24 2024
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で数学の…
Apr.30 2024
第11回今後の教育課程、学習指導及び学習評価の在り方に関する有識者会議について
4月26日に文科省で開催され…
Apr.28 2024
「プラスエリートクラブ」ページ更新のお知らせ
「プラスエリートクラブ」で数…
Apr.23 2024
「プラスエリートクラブ」ページ更新のお知らせ
「プラスエリートクラブ」で数…
Apr.18 2024
「数学ラウンジ」動画公開のお知らせ
YouTube 数学ラウンジ…
Apr.14 2024
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で数学の…
Apr.14 2024
「プラスエリートクラブ」ページ更新のお知らせ
「プラスエリートクラブ」で数…





