

プラスエリートに関する意見・質問
- 数学の内容に関する意見・質問
- Q1. 特性方程式について
- p.664 に数列の漸化式 \(a_{n+1}=pa_{n}+q\) に対して, \(\alpha =p\alpha + q\) を「特性方程式」, \(\alpha\) を「特性解」とありますが, これは特性方程式とは言わないのではないのではないでしょうか。
- A1.
- はい。原則としては言いませんが, そのように書いてある書籍もあります。プラスエリートは, 40 年以上も前からある書籍 M を参考にしてありますが, そこにはそのようにありました。また, いくつかの書籍にはある, しかし一般的な言い方ではないので, ここでは「特性方程式ということもある」という表現にしました。「いうこともある」という意味は, 少なくとも誰かが言っているということなので正しいかとは思います。この件は校正者からも指摘がありましたが, 他の「その場限りの造語」と同じ感覚で使っています。
- Q2.
- 直線の一般形が、y=ax+bだと、x軸、y軸に平行な直線はなんなんですか?そして、接線問題でそのような直線が円などの接線だった場合はどうやって解くのですか?最初に断り書きを描くのですか?(2019.4.23)
- A2.
- この質問は、プラスエリートのどのページに対する質問でしょうか。また、具体的にどのような問題にお困りでしょうか。
- Q3.
- 早速ですがプラスエリートIIBのp155について質問させてください。
2^x+2^-x=tとおいて相加相乗平均によってtの動く範囲を求めるのは受験では定番かと思いますが、この部分を授業していたときに、本校の生徒で某T会に通っている者が「T会で、こういう問題は相加相乗によってtの動く範囲を出すと減点される。tの最小値が等号成立から2であるとわかっても2より大きい数をくまなくとりうるかはわからないからである。よって両辺に2^xをかけて実数解条件などでtの範囲を求めるべきだと教わった」というのです。そんな厳密な議論は入試の解答としては必要なかろうと答えましたが不安になりプラスエリートを探した結果、清先生も相加相乗平均で(あっさりと?)範囲を求めていて安心したしだいです。先生の長い受験指導暦の中で今回のような、「tの範囲を求めるために相加相乗を使うのは減点である」というような考え方を聞いたことがありますか?また、どのようなご見解をお持ちになられるでしょうか。(2019.5.29) - A3.
- ご質問に対して回答させていただきます。
まず、はっきりさせておきたいのは、「t の範囲を求める」ことと「t の最小値を求める」ことは別の問題です。t の最小値を求めるだけであれば、t の範囲を求める必要はありません。「相加平均と相乗平均」の関係で得られることは t の最小値だけで、t の範囲ではありません。プラスエリートIIB の解答編の p.155 の (1) の問題は「最小値を求めよ」ですので、相加平均と相乗平均の関係であっさりと終わります。これが t の範囲を求めるのであれば、その求めた最小値からそれよりも大きい値すべてをとることを言わなければなりません。これがその問題では必要ないのであっさりとなっています。
さて、t が 2 以上の値のすべてをとることを言うのであれば、\(t=2^{x}+2^{-x}\) が x に関して連続であることを認め、x が大きくさえなればtがいくらでも大きくなることについて触れればよいと思います。本当に厳しい採点であれば、t が x について連続であることまで示せと一部の人はいうかもしれませんが、例えば \(\displaystyle\lim_{x→0} 2^{x} =0\) などは指数関数が連続であることを認めているからこそ成立することで、指数関数が連続であることは普段は認めていること(ただし、証明は難しい)ですからそこを深追いはしなくてもよいと思います。
さて、T 会の主張ですが、言っていることに間違いはありません。相加相乗平均だけでは t の最小値は求められてもそれだけでは取り得る範囲を求めたことにならないのですから。ただし、そのために 2 次方程式の解の存在条件を持ち出すといささか大がかりという印象もあります。しかし、慎重な人を非難するわけにはいかないのでそれはそれでその主張は認めなければならないと思います。 - Q4.
- 的外れな質問かもしれませんが、p373の下から6行目に「有理数xに対しa^x (a>0)を定義しよう.」とありますが、仮にa<0やa=0の場合を定義した場合はどうなるのでしょうか。ちょっと疑問に思って考えてみて、何か変なものになりそうですが、よくわからないので質問させていただきました。(2019.7.15)
- A4.
- 例えば \(a=-4\) の場合 \(x=\frac{1}{2}\) であれば、\(x=\pm 2i\) (一つには決まらない) ということも可能ですが、\(a\lt 0\) であり、\(x\) が無理数の場合は、高校数学流では一般的な定義はできません。\(a=0\) の場合も \(x=0\) の場合は定義はせず、状況によって都合の良い解釈をすることをします。
- Q5.
- おそらく誤植の報告
448ページの13行目にある「x→0のとき」が「h→0のとき」かと。(2019.8.11) - A5.
- ご指摘ありがとうございます。
確かにご指摘通り、該当箇所は x→0 ではなく h→0です。 - Q6.
- p259例題2-33の解答で、「逆に円(x-3)^2+y^2=4上の任意の点は条件を満たす」と書いていないのはなぜですか。(2019.11.22)
- A6.
- PA>0, PB>0 であることを認めれば、その条件下ですべて同値変形をしているからです。本当は ⇔ をすべての式の前につけて変形すれば問題はありません。
教科書では、1社のものだけが、「逆も成り立つ」と記すように書かれていますが、「逆も成り立つ」を主張するのならば、その理由も書かなければならないと考えています。「逆も成り立つ」を書くと指示をされた場合は、指示をした人がどこかの変形が同値変形でないか、それが自明でないという主張です。 - Q7.
- p920の(1)の解答で、n個のボールがk番目の箱を除くn-1個の箱に入る確率を求めればよいことは納得したのですが、P(Ak)=(1-1/n)^nと計算できる理由が分かりません。(2020.1.24)
- A7.
- \(n\) 個のどのボールも \(k\) 番目には入らない確率を求めます。どのボールも \(k\) 番目以外の箱に入る確率は, \(1-\frac{1}{n}\) です。\(n\) 個のボールは無作為に入れられるので、他のボールに独立に入れられると考え、\(1-\frac{1}{n}\) を \(n\) 個かけて \((1-\frac{1}{n})^n\) となります。
- Q8.
- p.70にある不等式|x+y|≦|x|+|y|を「三角不等式」と呼ぶのはどうしてですか。名前と形からすると、「三角形の成立条件」と何か関係(一方から他方が導ける、など)があるのでしょうか。それともこの二つには数学的なつながりはないのでしょうか。(2020.2.17)
- A8.
- 三角不等式の起源まではわかりませんが、多く言われていることは、三角形 ABC において \(\rm{BC}\lt \rm{CA}+\rm{AB}\) が成り立つこと、3 辺の長さを \(a\), \(b\), \(c\)で表すとき \(a\lt b+c\) が成り立ち、これをベクトルの形で表すと、\(|\vec{\rm CA}+\vec{\rm AB}|\lt |\vec{\rm CA}|+|\vec{\rm AB}|\) となることから、このような不等式を三角不等式と呼ばれるようになったと考えられています。
実数 \(a\), \(b\), \(c\) が「三角形の 3 辺の長さである」ことと、3 つの三角不等式「\(a\lt b+c\) かつ \(b\lt c+a\) かつ \(c\lt a+b\) 」が成り立つことは同値です。 - Q9.
- p986~p987の(注)について2つ質問です
・p987 4行目からの“Z⊂Xでなければ”というのを“Z⊃Xならば”と置き換えても同内容でしょうか?
・g◦fが定義できてf◦gが定義出来ないような関数fと関数gの具体例を思いつけなかったので出して頂きたいです。(2020.2.25) - A9.
- 最初の質問ですが、まず整理しましょう。ここでは、\(f\circ g\) について考えています。\(g\) は \(Y\) から \(Z\) への写像ですので、\(g\) によってうつされた像は集合 \(Z\) の要素です。これを次に \(f\) でうつすのですが、\(f\) は \(X\) を定義域とするので、\(Z\) が \(X\) の中に入っていないといけないということで、\(Z\subset X\) ということになっています。\(Z\supset X\) では定義できませんが、\(Z\supset X\) でなくても定義できない場合があるので、\(Z\supset X\) が定義できないことの条件にするのはよくありません。例えば、\(Z\cap X\) が空集合でも \(f\circ g\) は定義できなくなります。
次の質問です。
\(f\) は実数 \(x\) を \(x\to 2x\) によって対応させる写像、\(g\) は実数 \(x\) をベクトル \((x,1)\) に対応させる写像とします。この場合は、\(g\circ f\) は定義できますが、\(g\) の像がベクトルなので \(f\circ g\) は定義できません。 - Q10.
- 解の変換をする理由が説明されているページを教えて下さい。自力では見つけれず質問させていただきました。(2020.4.4)
- A10.
- 「解の変換」とは何を指しているのでしょうか。実際にそれが行われている場面を教えていただければ回答できるかと思います。
- Q11.
- 102ページの116の(1) 式変形をして左辺ー右辺≦0を示して-(a-b)の二乗≦0の証明でもいいでしょうか?また受験数学において定理などの証明は理解だけでなくゼロから導出できるようになるべきでしょうか?(2020.4.18)
- A11.
- 最初の証明について
途中の式変形が正しければかまいません。
次の質問
一部の定理は高校の範囲内で証明することが困難なものもありますが、プラスエリートの中で証明が書かれていているものについては、導き出せるのがよいと思います。結構、厳しいですが、それが理想です。 - Q12.
- p.29例題1-7について次のように考えました。両辺に(x-a)(x-b)(x-c)をかけてx^2=(x-b)(x-c)A+(x-a)(x-c)B+(x-a)(x-b)C ・・・? ?の両辺にa,b,cを代入するとa^2=(a-b)(a-c)A b^2=(b-a)(b-c)B c^2=(c-a)(c-b)C A,B,Cについて整理すると A=a^2/(a-b)(a-c) ・・・? B=b^2/(b-a)(b-c) ・・・? C=c^2/(c-a)(c-b) ・・・? となる。もし与えられた恒等式が初めから?であれば、一致の定理からこの解法で問題ないと思うのですが、実際に与えられた恒等式は、x≠a,b,cについてのものです。したがって、解答の中で「x=a,b,cを代入する」ことはまずいのかな?と思いました。自分なりの精一杯考えたのは次の通りです。この解答を逆から考えていく。?かつ?かつ?のとき、?はすべてのxについて成立する。よって、?、?、?は「?が」恒等式となるようなA,B,Cである。そして?が恒等式であれば、両辺をともに(x-a)(x-b)(x-c)で割ってできたx^2/(x-a)(x-b)(x-c)=A/(x-a)+B/(x-b)+C/(x-c)も、a,b,cを除くすべての実数について、xの恒等式となる。よって?、?、?が求めるA,B,Cである。というものです。この議論の通り、与えられた式がx≠a,b,cについてのものでも、整理してからx=a,b,cを代入するのは問題ないでしょうか?(2020.4.21)
- A12.
- 文字化けをしているため、質問の解読ができません。文字化けをしている部分の表現を変えて再度質問してください。
- Q13.
- 260~261ページ例題2-34の中の、「?を?に代入した後、さらに?を変形し?に再び代入する」というプロセスがどうにも腑に落ちないというか違和感を覚えてしまうのですが、このような代入はなぜ正しいのでしょうか。些末かつ漠然とした質問ですが、お答えいただければ幸いです。(2020.4.21)
- A13.
- 文字化けをしているため、質問の解読ができません。文字化けをしている部分の表現を変えて再度質問してください。
- Q14.
- P274にてα,βが二次方程式t^2-xt+y=0の解として与えられるということですが、このようにいつも定数がある場所に変数が置かれている形の二次方程式を初めて見たためモヤモヤしています。何か不自然な気がしてならないのですが、どのように捉えれば良いのでしょうか。おんぶにだっこな質問で恐縮なのですがご教授いただければ幸いです。(2020.4.22)
- A14.
- \(\alpha +\beta =x\), \(\alpha\beta =y\) であるから、\(\alpha\), \(\beta\) は2次方程式 \(t^2-xt+y=0\) の2解であることは、今後よく使いますので慣れていた方がよいと思います。
これは、\((t-\alpha )(t-\beta )=0\) を展開して得られます。 - Q15.
- P280(2)にて、α,βはt(>0)の二解であるのでα>0かつβ>0でないといけない(つまり求める条件はα+β>0かつαβ>0のみ)のではないか、と考えたのですがなぜこれは誤りなのでしょうか。(2020.4.22)
- A15.
- 直線 \(l_{t}\) が点 \((x,y)\) を2回通る必要はないからです。\(t\) は直線がいつ点 \((x,y)\) を通るときの値ですが、\(\alpha \gt 0\), \(\beta \lt 0\) の場合は、\(t=\alpha \) のときに \((x,y)\) を通っていることになりますので、そのような点 \((x,y)\) は通過範囲としてカウントされます。
- Q16.
- 問2-14(1)と例題2-26(3)について質問です。x≧0,y≧0の範囲を図示してからx軸,y軸に関して折り返そうと考えました。境界はx-y=1ですがy≧0かつ0≦x<1の範囲には直線が存在しないため0≦x<1は領域に含まれないと解答しました。また、例題2-26(3)の(?)においても、y<0,x≧1の範囲には曲線が存在しないため、領域には含まれないと解答しました。なぜこれらは誤りなのでしょうか。(2020.4.26)
- A16.
- どちらも (x,y の式)=0 が境界になるという発想なので、間違えてしまいます。例えば \(x^2+y^2\geqq 0\) などは境界がありませんが、この不等式が表す範囲は存在して平面全体となります。
- Q17.
- p.955 例題9-10(2)で、問題文に「信頼度95%」が書かれていませんが、解答では信頼度95%で考えています。(1)からの流れで暗に95%で考えると誘導されるようには思いますが、(2)でも「信頼度95%の信頼区間」と断っておいたほうが良いのではないかと思いました。(2020.4.26)
- A17.
- これはご指摘の通りだと思います。(1) の中での「信頼度95%」なので、(2)でもそう考えるのかは、一般的には自明ではありません。
(2) の問題文の冒頭に「信頼度95%の」を入れておくように訂正表にも書いておくことにします。 - Q18.
- P293大問10(2)について、解答解説のP96で絶対値記号を二乗して外していますが、k≧1/3の場合とそれ以下の場合に分けて考え最終的に1/3≦k≦3/4とするのが正しいのではないでしょうか?(2020.4.29)
- A18.
- このままでも正しいのですが、\(k\geqq \frac{1}{3}\) とそれ以外に分けてもかまいません。その場合であっても、その不等式の解は、\(0\leqq k\leqq \frac{3}{4}\) になります。例えば、\(k=0\) は元の不等式を満たします。
- Q19.
- 29ページ例題1-7について質問です。問の本題からは逸れますが(恒等式の定義に関するような質問です)、式番号(3)では「すべてのxで両辺の値は一致する」とあります。(3)から(1)に目を向けたとき、(1)⇔(2)⇔(3)かつx≠aかつx≠bかつx≠cですから、恒等式(1)の両辺は「x≠a,x≠b,x≠cで一致する」と考えてよろしいのでしょうか。(2020.5.3)
- A19.
- はい。それでよいと思います。
- Q20.
- p.1000の円と放物線が接する条件について、重解条件で得られたk=-5/4に何か図形的な意味はあるのでしょうか。円と放物線が2点で接することがない場合にこの値が一体何を表しているかが分かりません。(2020.5.5)
- A20.
- 実数の世界で考えている限りは特に意味はありません。
- Q21.
- 一次独立と一次結合の違いは何ですか?(2020.5.9)
- A21.
- どのあたりを見てその疑問を思いついたのでしょうか? それにそって説明します。
- Q22.
- P755のように、一次結合は2つのベクトルによって表すことで、一次独立はP765【2つのベクトルの1次独立の定義】によって一次結合で表されたベクトルが1つに決まるという性質で、2つのベクトル(ベクトルaとベクトルb)を司るということでしょうか?(2020.5.10)
- A22.
- 部分的によいと思いますが、1次結合、1次独立といった概念は、2 つのベクトルだけの話ではありません。3つのベクトル、4つのベクトルにもあります。
1次結合は、表現の問題で、与えられたベクトルを実数倍したものの和の形のことをいいます。1次独立は、ベクトル間の関係を表す用語です。 - Q23.
- p79 7行目あたり「となる.また,n=k+1の場合の…」とありますが、これはm=k+1の間違いではないでしょうか。(2020.5.13)
- A23.
- 申し訳ございません。これはご指摘の通りです。
- Q24.
- p.80 11行目 α^(2^m)=x_1x_2・・・x_nα^((2^m)-2) とありますが、この=は≧ではないでしょうか。(2020.5.19)
- A24.
- ご指摘の通り ≧ です。訂正表を更新しておきます。ありがとうございます。
- Q25.
- p.81 手順2による証明では等号成立条件について触れられていません。もし手順2の帰納法で等号成立条件がx_1=x_2=・・・=x_nのときであることも一緒に証明するのであれば、n=k+1のときに等号が成立する、すなわちf_(k+1)(x)=0となるときは、x=αかつ下から5行目の等号が成立するときを考えてx=α=(x_1x_2・・・x_k)^(1/k)かつx_1=x_2=・・・=x_kのときだからx_1=x_2=・・・=x_k=xのとき。よってn=k+1のときも成立。といった具合でいいのでしょうか。(2020.5.19)
- A25.
- ご指摘の通りです。それでよいです。訂正表を修正しておきます。ありがとうございます。
- Q26.
- 多項式と共通解に関する質問です。(以下登場する式はすべて多項式です)「f(x)をg(x)で割ったときの余りをr(x)とすると f(x)=g(x)Q(x)+r(x) が成り立ちf(x)=0かつg(x)=0を満たす共通解が存在するとすれば,それはr(x)=0の解の中にある」ここまでは納得できました。しかしr(x)=0の解x=αがf(x)=0の解になっているかを確認する(十分性の議論)ときにQ(α)≠0に注意する理由が分かりません。Q(α)=0となってしまった場合,どのような不都合が生じるのでしょうか。(2020.5.23)
- A26.
- 具体的に、プラスエリートIIBのどこを見ての質問でしょうか。どこを見たかに応じて答えていますので、それを記していただけると答えられます。
- Q27.
- お忙しいと思いますが、誤植を見つけましたので報告させていただきます。P.376の一番下に書かれている極限の性質に関する注釈(6)のところですが、数列b(n)の方はlim(x→∞)ではなくて、lim(n→∞)ではないでしょうか?正否のご検討宜しくお願い致します。(2020.6.1)
- A27.
- ご指摘の通りです。誤植については申し訳ございません。
- Q28.
- 782ページ9行目から10行目にかけての式変形についてです。内積の計算なのに通常の積のように計算出来るのはなぜなのでしょうか。補足の説明は理解出来ましたので、最終的に内積の値がa1b1+a2b2となることはわかるのですが…(2020.6.24)
- A28.
- その部分は、p.780 の内積の性質 (1), (3) を使っています。内積の分配法則を用いて変形しています。
- Q29.
- P.E.数IIBにある図形と方程式の束の考え方について二点質問です、以下陰関数f(x.y)等をFと書きますm(_ _)m ?p204 注の8行目~の文章についてです この部分は p・F+q・G=0(ただし、pもqも定数(実数)かつp^2+q^2≠0) の形でも “F=0もG=0も円の方程式であるとき、2曲線の交点を通る例えば3次関数のようなものは表せない“という解釈であってますでしょうか? ?またこの解釈であってたとき、p199 7~10行目のP・F+Q・G=0 のようにp,qが定数でなくて多項式で(下の注釈22)を満たしていれば“F=0もG=0が円の方程式でも2曲線の交点を通る例えば3次関数のようなものも表せる”という認識は間違えでしょうか?(2020.7.5)
- A29.
- \(p\cdot F+q\cdot G=0\) の形では、3次式になりませんから、3次関数のグラフにはなりません。
また、\(P\cdot F+Q\cdot G=0\) の形でも \(x^{3}\) を作ろうとすると \(xy^{2}\) の項ができてしまい、この項を消そうとするとまた余分な項ができますから3次関数のグラフは無理ではないでしょうか。 - Q30.
- p415 注の3~4行目について質問です 私はこの文章を「f=gが成り立つとき、その両辺が正の値であるかについて、fとgは同じ値をとるので片方の辺の式が0より大きければもう一方も0より大きい事が保証されるので条件として付加するのは片方でもいい」と解釈したのですが、例えばp417の例題(2)、(3)において条件を省こうとすると答えが求まらない場合があり混乱しております。恐らく解釈が間違っているのではと思っているのですがどこが違うか見当つかないので助けて頂きたいです。(2020.8.9)
- A30.
- 解釈は正しいです。p.417 については、完全に \(\log_{2} A =\log_{2} B\) の形になれば大丈夫です。
- Q31.
- p583下から五行目の「定義域内の任意の値で等しい」という部分について質問です。条件6.19の一文目に条件6.21(両辺を微分した式)が相当し、「定義域内の任意の~」という部分は条件6.19の二文目に相当すると考えたのですが、その場合「定義域内の任意の値で等しい」ではなく「定義域内で等しい値が存在する」などになるのではないのかな、と思いました。お忙しい中恐れ入りますが、簡単にでもお返事いただけると幸いです。(2020.9.27)
- A31.
- その通りです。\(f(x)\) と \(g(x)\) は定義内のどこか一つの値で等しいということです。そのどこか一つが「どこでもよい」という意味で「任意」と書いたのですが、指摘された箇所ではそのように読めずに誤解を与えることも十分に考えられますから、次の修正のときには、検討したいと思います。貴重なご指摘ありがとうございました。
- Q32.
- p853の注2、p850~ 例題8-30について2つ質問です。
1.vec{a}=vec{b}→vec{a}?vec{c}=vec{b}?vec{c} の逆は後件が|vec{a}|=|vec{b}|と同値なので一般に成り立たないことは分かったのですが、例題8-30 (2)の別解p853の上から8~9行目辺りで上記を用いて出た結果から解を求めることが出来たのは『3つのベクトルが一次独立より空間内で?を満たすt,u,vは唯一通りのみ存在する』という事が言えたからでしょうか?
2.それと、p854の例も見て思ったのですが一般に上記の逆を用いて解を求める事ができない時、解答の場合のように各成分を比較する方法でも解を求めることができなかったりするのでしょうか?(2021.1.6) - A32.
- 1.については、ご指摘の通り「3つのベクトルが一次独立であるため、t,u,vがただ一つ存在することはわかっている」というのが前提です。
2.各成分を比較する方法は有効です。ただ、成立しない場合は、t,u,vも求められない、すなわち「解なし」の状態で出てきます。 - Q33.
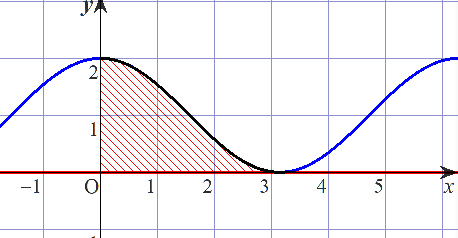
- p541の問6?10の(2)の答えがなぜπとなるのですか?(2021.1.17)
- A33.
- その積分が表す面積は、図の斜線部です。この \(y=1\) より上の部分を切り取って、\(y=1\) より下の部分の \((\frac{\pi}{2}\leqq x\leqq\pi )\)にはめ込むとちょうど横の長さ \(\pi\)、縦の長さ 1 の長方形になり、この面積が \(\pi\) となります。これが積分の値なので答は \(\pi\) になります。
- Q34.
- 初版第1刷の803ページ図の下の記述です。点Pが点Aと一致する場合はベクトルAPとベクトルnは垂直とはならないのではないでしょうか。内積が0はよいのですが。(2021.1.20)
- A34.
- \(\vec{\rm AP}\) が \(\vec{0}\) になる場合の記述についてですが、そのような指摘はいろいろな場面であてはまります。
\(\vec{0}\) の向きという場合に、「考えない」という立場と「任意の向きを向く」という立場があります。後者の立場であれば問題はありません。一方、分けて書くこともあります。
同じ様な場面はあげるときりがなく、例えば、\(\rm AB\) を直径の両端とする円のベクトル方程式を \(\vec{\rm AP}\cdot\vec{\rm BP}=0\) とするときも、\(\rm AP\) と \(\rm BP\) が垂直だからで流す場合もあります。2つのベクトルが1次独立である場合も2つのベクトルが平行でないことで終わらせることもあります。それは、専門書では読み手がうまく読むようにしていると思うのですが、うまく読めない場合があれば、質問をするとよいと思います。 - Q35.
- p464 例題5-6?の解答についてです.与えられた3次函数は点(0,1)を通りますが,グラフでは原点を通過しているのは誤植だと思います.(2021.1.27)
- A35.
- ご指摘の点はもっともです。ただ、プラスエリートの図はほぼすべて正確なものをアプリを使って描かせており、この図も例外ではありません。この図は、実は原点を通っていないのですが、線の太さの関係で通っているように見えてしまうということになっています。
原因は縦軸を圧縮しているからです。もちろん図の描き方としては、本物では特徴がわからないので、特徴がわかるように図を変えて描くという方法もありますが、プラスエリートの方針では、「放物線はつねに本物の放物線を見ていてほしい」というものがありまして、いまのところはこれで統一しています。 - Q36.
- P697 の21番目の注に工夫次第で、整数あるいは有理数に関する命題にも適用できる場合があるとありますが、それの例としてはどのようなものが挙げられるのでしょうか(2021.2.12)
- A36.
- 整数全体の証明に応用する場合はいろいろあると思います。例えば、\((\cos\theta+i\sin\theta)^{n} =\cos(n\theta)+i \sin(n\theta)\) (ド・モアブルの定理) が整数全体で成り立つことを示す場合がその一つです。
先に、自然数の場合を示しておいて、あとで、\(n\lt 0\) の場合を \(n=-m\) に置き換えて示すこともできれば、\(n=-1\) をまず示し、\(n=-k\) が成り立つことを仮定して \(n=-(k+1)\) の場合を示すことで解決できます。
有理数の場合は、有理数が 1 列に並べられることから原理的にはありうるのですが、有理数に関する証明は変数が実数だと考えても成り立つ場合が多いので、実数の場合を微分などを使って証明すれば解決できるので、有効な例はほとんどないと思われます。 - Q37.
- P586大問3北海道大学の問題の解答について質問です。解答・解説P231に記述されている「(4/3a?-b?)p=-bのときはb=0であれば?を満たすbは存在する」の意味が理解できませんでした。なぜ「pは存在する」ではなく、「bは存在する」なのでしょうか。よろしくお願いします。(2021.2.13)
- A37.
- ご指摘の通りです。ご指摘の部分は「pは存在する」が正しいです。訂正いたします。
- Q38.
- ベクトルの平行条件の記述がありません。これでは他の本をみなくてはなりませんが?(2021.3.5)
- A38.
- ベクトルの平行条件は、図形的な説明としては、2つのベクトルの向きが一致するか、逆を向いているかです。数式上では、一方が他方のスカラー倍で表されることが定義になります。(これは、p.763 ではすでに使われています。)
零ベクトルについては、「零ベクトルの向きは考えない」あるいは「零ベクトルの向きは任意の向きである」の両方の解釈がありますが、ケースバイケースでこのどちらかを出発点にしています。どちらを選んでも困ることはあまりありません。 - Q39.
- p433注にあるx→∞はx→aではないですか。(2021.3.22)
- A39.
- 申し訳ございません。ご指摘のとおりです。
- Q40.
- p29例題1-7について質問です。プラスエリート数学1Aのp3の記述に「任意のxを代入してもつねに成り立つ式をxの恒等式という」とあります。しかし、例題1-7の与恒等式?はx=a,b,cでは成立しないので恒等式とは言えないのではないでしょうか?それとも「等式?は高々3つを除くすべてのxについて成立するのでxの恒等式である」という解釈でしょうか?よろしくお願いします。(2021.3.31)
- A40.
- 最初の式番号 1 の式を恒等式と呼んでいますが、「任意の x を代入する」場合は、定義される(式が意味をもつ)ような「任意の x」です。
ですので、後者の解釈でよいです。 - Q41.
- p43の内容について、本書では√-19=√19iを定義していないように思えるのですが、これは自明なこととして扱っているということですか?(2021.4.9)
- A41.
- 自明ではありません。次に修正をいれるときには定義しておこうとおもいます。
- Q42.
- P766(ベクトル)の問8-6について,答えはa=2となるようですが,この回答を導く方法がわかりません.機会がありましたら,問い解説動画で解説をいただけると幸いです.(2021.4.11)
- A42.
- これは、二つのベクトル \(a,b\) が平行になる条件から求めるものです。平行条件から
\(2a(a+4)-3\cdot 4a =0\)
を作り、ここから求めます。
これについてはリクエストに応えるように優先的に動画を作ります。 - Q43.
- P12の多項式の割り算の話についてですが、恒等的に0でないとはどういう意味でしょうか?恒等式の=、関数の=(f(x)=~)や4+6=10の=は意味が違うのでしょうか?そうであれば違いや等号の扱い方(行って良い変形等)などを教えていただきたいです。(2021.4.16)
- A43.
- 記号「\(=\)」は単に「等しい」ということしか表しません。種類があるわけではありません。
その場面でいう「恒等的に \(Q_{1}(x)=Q_{2}(x)\)」とあるのは、「すべての \(x\) で \(Q_{1}(x)=Q_{2}(x)\)」の意味です。 - Q44.
- 例題1-5(1)で質問です 条件よりf(x)=(x-α1)(x-α2)(x-α3)…(x-αn)Q(x) とできる。これはまさしくφn(x)の倍数であるからf(x)はφn(x)で割り切れる。ではダメなのでしょうか?(2021.4.16)
- A44.
- ここでは、まさに「条件より f(x)=・・・・とできる」を証明せよという問題なので、証明すべき内容を証明につかっているのでまずいです。
- Q45.
- Q44の者です。「AならばB」を示せという問題は、Aという条件は既知のもの(語弊を恐れずいうなら公理のように)として扱い、そこからBという結論を導けば良いものだと思っていたのですが間違いでしょうか?「「f(α1)=…=0」であれば」という部分からf(x)が因数分解できると話を進めたのですが、問題文のどこを読み間違えているのかわかりません。また、どうしてこの問題で帰納法を使おうと思ったのかという発想の元があれば教えていただきたいです。(2021.4.17)
- A45.
- 仮定 A の件は間違いではありません。ここでは、そのような問題ではないということです。つまり A ならば B を示すときに、A を既知としてよいかどうかが問題ではありません。因数定理は、あくまでも一つの数に対しての主張で、\(f(\alpha)=0\)であれば、\(f(x)\) は \((x-\alpha)\) を因数にもつことは認めます。しかし、\(\alpha\) が、\(\alpha_{1}, \alpha_{2}, \cdots\) のようにたくさんあっても同じようなことが言えるかどうかを確認しているのです。一つで言えるから二つでも言えるとしてよいのかということです。事実、\(\alpha_{1}\) と \(\alpha_{2}\) が「異なる」という条件がなければ言えません。
- Q46.
- P97例題1-26について質問です。コーシーシュワルツの不等式から-√14≦P≦√14…(1)を出したあとの答案で「ここでx=±1/√14 y=±2/√14 z=±3/√14(複号同順)はx?+y?+z?=1満たし、かつ、(1)の不等式において等号が成立する。従って最小値-√14 最大値√14」としても大丈夫ですか?(2021.4.17)
- A46.
- かまわないです。できれば、複号のどちらが、2つあるどちらの等号を成立させるかを言及するとなおよくなります。
- Q47.
- P190例題2-16,17のようなグラフをかけという問題ですが、実際の答案に定義域ごとに場合分けした式や「~はx軸に関して折り返したグラフである」のような説明を記述をする必要はありますか?計算だけ計算紙等に済まし、答案にはいきなり座標とグラフを書いて、軸との交点の座標と、各直線(や曲線)の式を添えるだけでは、不十分な答案になりますか?(2021.4.18)
- A47.
- 数学的な事実を理解することと答案に書くべきかどうかは少し違います。答案でどう判断されるかは採点者のさじ加減のところもありますから、こうすれば絶対大丈夫というようなことはありません。答案の説明が不十分かどうかを決定するのは採点者側なので、どのような採点をされてもよいように説明をしておくのが安全です。
- Q48.
- p232例題2-26で分数関数と円が接しているという情報は連立して初めてわかる事実ですか?問題集などの奇跡の問題における解答では、交点や接点の座標をさらっと書いているものが殆どですが、やはりこれらも解答に書いていないだけで、裏では連立することにより確かめているのでしょうか?(2021.4.19)
- A48.
- 非常に重要な質問です。本当はここは調べなくてはわからないことです。例えば、数値が少し違っているだけで接していなくなります。
その問題を解く本題からはずれるので、そういう部分は本題より目立たないように書いたりしますが、答案に「書く」「書かない」に限らず自分で調べる癖をつけましょう。
今回、どのように求めたかは補足のような感じで説明してありますが、もちろん堂々と書くと採点のときに好感が持たれると思います。
さらに、こういうことに「気になる」ようになるのは上級者への入り口なので、他の問題でも気にしてください。 - Q49.
- p240で半円と直線が共有点を持つことの必要十分条件について,なぜ(ii)を加えるだけで必要十分になるのかわかりません。また,私は半円y=√1-x ^2と2x+3y=kを連立させて,これが実数解を持つとして判別式を利用したのですが,-√13≦k≦√13しか出てこず失敗しました。何がいけなかったのでしょうか?(2021.4.19)
- A49.
- なぜ(ii)を追加することで必要十分といえるかについては絵を使った説明が必要になるので、プラスエリートの問いの動画「問い2-16」の中で、「発展」という項目を作り説明しましたので、そちらを参照してください。
また、「こうやったけれど出なかった」という質問は、具体的にその中を確かめてみなければ答えられません。少なくとも示された方針を正しく処理すれば正しい答はでます。 - Q50.
- 第5章微分法p454の11にある「h→0とする際にg(x+h)-g(x)=0が無限回現れる関数は存在する」の「無限回現れる」の部分がよくわかりませんでした。どこに無限回現れるのでしょうか?(2021.5.2)
- A50.
- これは、\(h\) が 0 に限りなく近づくときに、\(g(x+h)-g(x)\) が 0 になることが有限回ではないという意味です。「どこに?」と言われれば、\(\frac{f(g(x+h))-f(g(x))}{g(x+h)-g(x)}\) と書かれている「分母に」ということになります。
極端な例が \(g(x)\) が定数の場合ですが、定数を除いても \(g(x)=x \sin(\frac{1}{x})\) などがあります。これは、「プラスエリートIII」の p.851 に詳しく書かれてあります。
プラスエリートII・B
最新記事
Feb.14 2026
第6回算数・数学ワーキンググループについて
2月13日に文科省で開催され…
Feb.03 2026
第14回教育課程企画特別部会について
2月2日に文科省で開催された…
Jan.23 2026
第5回算数・数学ワーキンググループについて
1月23日に文科省で開催され…
Jan.05 2026
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で『5 …
Jan.04 2026
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で『1 …
Jan.03 2026
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で『1 …
Dec.28 2025
「数学ラウンジ」動画公開のお知らせ
YouTube 数学ラウンジ…
Dec.25 2025
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で『10…
Dec.23 2025
第4回算数・数学ワーキンググループについて
12月22日に文科省で開催さ…
Dec.17 2025
新刊のお知らせ
新シリーズ「数学の受験教科書…
Dec.15 2025
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で数学の…
Dec.13 2025
第3回算数・数学ワーキンググループについて
12月12日に文科省で開催さ…
Dec.01 2025
新刊のお知らせ
新シリーズ「数学の受験教科書…
Nov.25 2025
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で数学の…
Nov.22 2025
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で『8 …
Nov.15 2025
第2回算数・数学ワーキンググループについて
11月14日に文科省で開催さ…
Nov.09 2025
「エチュードクラブ」ページ更新のお知らせ
「エチュードクラブ」で戦略編…
Oct.19 2025
第1回算数・数学ワーキンググループについて
10月17日に文科省で開催さ…
Oct.12 2025
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で数学の…
Oct.07 2025
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で『6 …





