数学教育研究所公式サイト

プラスエリートに関する意見・質問

数学の内容に関する意見・質問

プラスエリートI・A

Q1. p.62 例題 1 -- 18 について: p.62 例題 1 -- 18 (2) について, $x=1$, $100$ を反例に挙げていますが, 例えば $x=1-y$ は任意の $y$ に対して $x+y\gt 0$ を満たすのではないでしょうか?
A1.: (2) の, $P_{2}: \exists x\{ \forall y\ x+y\gt 0\}$ をもう少し詳しく言うと次のようになります。
「次のような(実数) $x$ が存在する。それは, どのような実数 $y$ に対しても $x+y\gt 0$ となるような $x$ である。」
大切なことは, $x$ を先に決めて固定してしまうということです。$x$ を先に決めて固定したあとに, どのような $y$ をもって来てもつねに $x+y\gt 0$ が成り立つ, そのような $x$ はあるかということを聞いています。
　この問題の解答が「偽」になっている通り, そのような $x$ は存在しません。つまり, どのような $x$ を選んでそれを固定しても $y$ として後から $y\lt -x$ となるように選べば $x+y\gt 0$ とはならなくなります。
　ちなみに, $x=1$, 100 は「反例」ではありません。$x=1$ のときはダメですね。$x=100$ のときもダメですね。これがダメになるようにどのような $x$ に対しても「すべての $y$ で $x+y\gt 0$ となる」ことはないからダメですね, と言っているわけです。
　質問の「$x=1-y$ とすれば・・・・」というのは, $y$ に応じて $x$ を決めるので, それは,

$\forall y\ \{\exists x \ x+y\gt 0\}$　(これは真. ただし, $x$, $y$ は実数)
に対する例となっています。
Q2.: 写像については二次関数の導入のところを読んだのですが、例えば、y＝axで、y＝f(x)とすると、xが定まるとyが定まると書いてありましたが、aも定まらなければyは定まらないと思うのですが。aは定数であるから、無視するという考えならば、そもそも未知数、定数、変数についての定義を教えて下さい。(2019.3.29)
A2.: 　回答ということではないですが, 具体的に二次関数の導入のどのあたりを読んでそのように思えたのでしょうか。
　一般的な答え方になりますが, 「未知数」は方程式などで「値がまだわかっていない数」, 定数は「固定された数」とか「ある文字に注目したときにその文字に依存しない数」、「変数」は「あることがらに注目したときにいろいろな値をとる数」です。
Q3.: 集合の分野で「空集合はすべての集合の部分集合である」というのがイマイチよく分からないです。言葉の意味が分からないというよりも、そうなる必然性というか、数学的意味がピンとこないです。もう少し具体的に言うと、空集合がすべての集合の部分集合だと、そうでない時と比べて何が起こりうるのか。そもそも、教科書に載っているようなことから演繹できるようなことなのか。ご指導頂けると幸いです。(2019.4.7)
A3.: 質問者の学年あるいは学習到達度が見えませんので(特に述べなくてもかまいません), 少しきっちりとした説明をしてみます。
　まず, 「集合 $A$ が集合 $B$ の部分集合である」ことの定義は,
　　任意の $A$ の要素は $B$ の要素である
すなわち,
　　$\forall x\ (x\in A\ \Rightarrow\ x\in B) \qquad \cdots\cdots\,(★)$
が成り立つことです。$A$ が空集合の場合は $x\in A$ である $x$ が存在しないので, (★) は成立するので, 「空集合は任意の集合の部分集合」ということになります。(命題「$P$ ならば $Q$」について, $P$ を満たすものが存在しない場合はこの命題は真になるというのと同じです。)
　もう少し補足します。(★) が $A$ が $B$ の部分集合であることの定義ですが, 逆に $A$ が $B$ の部分集合ではないとはどのようなことかというと, (★) を否定すればよいので,
　　「少なくとも一つ $A$ の要素であるが $B$ の要素ではないものが存在する」
すなわち,
　　「$\exists x$　($x\in A$ かつ $x\in\!\!\!\!\!\backslash\; B$)」
となります。$A$ が空集合の場合は $x\in A$ である $x$ が存在しないので, 「$A$ の要素で $B$ の要素ではない」ものは存在しません。つまり, (★) の否定が成立しませんので, $A$ が空集合の場合は, 任意の集合 $B$ の部分集合ということになります。
Q4.: |3xー6|>2x+4 のような問題は、3x－6を場合分けして、解く方法は理解しています。では、なぜ定数の場合のように、|fx|>3?－3<fx<3のように出来ないか？実験してみると、このやり方で出来る問題もありますが、出来ない問題もあったりします。(2019.5.5)
A4.: プラスエリートのどこの記述を見ての質問でしょうか?
Q5.: p6の絶対値の性質の3.の記述についてなんですが、これは同1.に適用できて逆も成立しないのでしょうか？(∵絶対値a≧0)(2019.5.28)
A5.: 一般に、A⇒Bとある場合は、AならばBを言っているにすぎず、逆が成り立たないとまで言っているわけではありません。すなわち、「A⇒B」とあれば、「B⇒A」は成り立たないとまで言っているわけではありません。ご指摘の 3. は逆も成り立ちます。また、|a|≧0なので、3. を1. に含めることも可能ですが、|x|=|a| の形で現れることもありますので、別の式として書いておきました。独立な事項であるわけではありません。
Q6.: 解答・解説 p.156 章末問題8の解答について
p.156の中程から抜粋「x(k)=0,1,2,3(1≦k≦n)を満たす{x(n)}(k=1,2,…,n)の組の個数」の表すものが分かりません。解説お願いします。(2019.6.14)
A6.: 例えば、$n=5$ くらいで考えてみましょう。
この場合は、$X_{n}$ (以下 $X$ で表す) が 8 以下になる確率を求めることになります。さて、$X$ が 8 以下になる場合ですが、すべて 1 のカードを取り出した場合でも $X=5$ となるので、$X\leqq 8$ となるのは、すべて1の場合と比べてあと3しか増えることが許されません。この増えた部分を $x_{k}$ で表しています。
例えば, 「3,2,1,1,1」の順にカードを引けば、$X=8$ であり $X\leqq 8$ を満たす。これを1より大きい部分を書き、「2,1,0,0,0」を考えることにしました。このとき、$k$ 回目に並んだ数を $x_{k}$ としています。
この $x_{k}$ はすべて0以上3以下の値をとり、 $$ x_{1}+x_{2}+x_{3}+x_{4}+x_{5}\leqq 3$$ を満たします。このような $ (x_{1}, x_{2}, x_{3}, x_{4}, x_{5})$ の組の個数が $X\leqq 8$ となる場合の数です。
この考え方を一般化して書いてあります。
Q7.: 例題６－３（３）についての質問です。
解答では、pk=1/9(10^n-1)を満たす正の整数k,nが存在することを示しています。このとき、１つ目の質問として、解答にはkの存在は明記されていますが、nの存在が明記されていません。解答としては、明記されていないので不十分なのかなと思いましたが、いったいどうしてでしょうか。
２つ目の質問として、解答での式?において、10^p-1 - 1=plを満たす正の整数lの存在が示されています。この時点で、p,lでkとnを表すことができ、正の整数k,nが存在することは示すことができるのでは無いかと思いました。よって、「ここで・・・」以下の解答を書く理由が理解できませんでした。その理由を教えて頂きたいです。(2019.6.29)
A7.: ご質問ありがとうございます。
1つ目の質問
確かに、p.423 の下の方でkとnの存在を示すと書いていながら、具体的にkとnの値を表現していないので読みにくいと思います。nについては、次のページを読めば、n=p-1 であり、kについては、l/9 ということになります。「示す」と言っておいてnに相当する部分が出てきてn=の形にしなかったのは読者に余計な負担を与えたかもしれませんので機会があれば追加して書くようにします。
2つ目の質問
今度は、逆に、問題文の形にこだわり、あくまで 111・・・11 =p×(整数) の形を作ったということです。ここで以下がないと、111・・・111 の形は出てこないから記しました。
Q8.: P56の例の(3)についてですが、aとbの値を決めずに、先にxの値をx＝1,-1とかx＝2^(1/2)×i,-2^(1/2)×iとか決めれば、命題の真偽が決まる（前者は正、後者は偽）ので、xについての条件と言うこともできるのではないでしょうか？(2019.7.25)
A8.: そこには、xの2次方程式が解をもつかどうかの条件と書いてあるので、xに何かを代入するのでは違うことをしていることになります。あくまでも x があるかどうかの問題です。
Q9.: p.49の注にある背理法に関して質問です。「あることがらPを証明するときに、Pを否定すると矛盾が生じること」が示せたときに「Pが成立する」として良い理由がわかりません。なぜせすか？(2019.10.19)
A9.: ここでの前提ですが、証明したいことは命題ですので、「正しい」か「誤り」のいずれか一方が必ず成り立つものを証明しています。このような場合「P」か「Pの否定」のいずれか一方のみが正しくなります。それは、「Pの否定」の定義が「Pと真偽が逆になる命題」であるからです。
したがって、「Pの否定」が否定された段階で、「P」か「Pの否定」のどちらかが正しいので、もう一方である「Pが正しい」となります。
Q10.: p.76 なぜ対偶は元の命題と真偽が一致するのですか？(2019.10.19)
A10.: p.65 に「p ならば q」の真理表が書いてあります。「p ならば q」の対偶「～q ならば～p」(～p は p の否定を表します) の真理表もこれに一致するのが理由ですが、これは次のように示せます。
「～q ならば～ p」が真になるのは、
q が成り立たない場合は必ず p が成り立たなくなる「q× かつ p×」の場合
そして、
「～q」を否定した q が成り立つ場合、すなわち「q ◯」です。このとき、p は◯でも×でもよいのです。これに基づいて「～q ならば～p 」の真理表を書くと、「p ならば q」の真理表と真理が一致します。
これが理由です。
Q11.: p.83 例にある「yはxの関数である」ことの定義は何ですか？xに対して１つのyを対応させる関係のことを関数と呼ぶのであり、このyはあくまで関係式を満たす数(もの)でしかないのではありませんか？(2019.10.20)
A11.: 「yはxの関数である」の定義は、その前のページに書いてある通りです。書き直すと、定義域内にあるすべてのxに対し、ただ一つの対応するyが終域内に決まるとき、そのxとyの関係をいいます。
関数 y=f(x) と書いたとき、この「y=f(x)」の部分は関数関係を表す式と呼ばれることもありますし、この式をもって話の前後によっては「変数yをxの関数である」としている本もあります。
Q12.: 「整式f(x)が～を満たすときの、f(x)を求めよ」という形の問題を解いていて、整式f(x)とある場合、xは必ず1次以上である必要があるのかと疑問に思い、整式の分野を調べました。単項式も多項式とみなされ、整式とは多項式であると書かれていたので、xの0次(定数)も整式f(x)の内に入るだろうと考えたのですが、その問題の解答ではその可能性は排除されていました。なので、整式f(x)とある場合の定義を教えていただきたいです。(2019.10.21)
A12.: 「整式」の定義についてですが、そもそも「整式」という用語は文科省用語とされ、その証拠に(というほどでもないですが)英語にこれに対応する言葉はありません。したがって、「整式の意味は文科省に聞いてください」というのが正しい対応かもしれません。
このようなこともあり、プラスエリートでは、「整式」という用語は用いていません。一瞬、整式という言葉を使ったかもしれませんが、基本的にそのような個所はすべて「多項式」という用語を用いてあります。ですので「整式」は管轄外というスタンスです。
とはいうものの、入試問題では「整式」という用語を使う傾向にあり、それは細かいところではローカルルールがあるなど様々です。
・整式とは多項式のこと (この場合単項式は多項式の特別な場合)
というのが多数であると思いますが、
・多項式は「多」の文字があるので、項が2個以上である。1つの場合は単項式という。そして、単項式と多項式を合わせて整式という。
このように考えている人たちも少なくありません。また、出版社によっては、長年この定義を採用しているので、今更変えられないというところもあり、このようなところに変更を求めると逆切れされてしまいます。
さて、いずれにしても定数は多項式ですから、どの解釈でも定数も整式になるはずです。どのような流れででてきた話か分かりかねますので、一般的な答えとしてはこのようになります。
Q13.: ｐ６８(3)の解説で、aを場合分けをして考えていますが、(2)と同じように,-1≦-aを満たせばよいので１≧aという回答はどうでしょうか。(2019.11.1)
A13.: $-1\leqq -a$ の場合には、$-a\lt x\lt a$ を満たす $x$ が存在する場合とそうでない場合があります。それによって成り立つ理由が異なりますので、やはり解答のように分けて書くのがよいかと思います。
Q14.: p54、節末問題(113)(1)の√6が無理数であることの証明ですが、解答は6n^2=m^2において、左辺が偶数だから～としていました。自分は、√2の証明における2の部分を6に変えて、左辺が6の倍数だから～としていました。この方法は間違っているのでしょうか？あえて偶数であることに言及されているのは意図のあることだと思うのですが、自分で考えてもわかりませんでした。よろしくお願いします。(2019.11.30)
A14.: 「左辺が偶数だから」としているのは、2 が素数だからです。この問題の場合、6 の倍数であるからとしてもうまくいくのですが、6 は素数ではないので、「$mn$ は 6 の倍数だから $m$, $n$ の少なくとも一方は 6 の倍数」は誤りですし、「$m^2$ は 8 の倍数だから $m$ は 8 の倍数である」も誤りです。素数の場合のときにつねに安全に議論できます。素数でないときは、それ以外の場合も気にしなければならないのであまり好ましい方法とは言えないでしょう。
Q15.: p123、節末問題(201)(1)の解説についての質問です。
　y=x^2-6x+3
　　=(x-3)^2-6
の一行目の＝と二行目の＝は異なる使い方をしている等号であることに注意することと書かれていますが、一行目のものが方程式の＝、二行目のものが恒等式の＝ということでしょうか？また、異なる使い方であると理解したうえで、何に注意を払えばよいのでしょうか？(2019.12.3)
A15.: そのような理解でよいです。異なる意味の「=」を混同して使うと長い式の場合は、理解ができなくなることがあります。この場合ならそれほど心配することはありません。書く人がわかっていればよいと思います。また、そのような書き方をしている書籍もあるかとは思いますが、特にコメントすることはありません。
Q16.: p143(208)の解説では、a<0,a=0,0<a<1,a=1,a>1で場合分けされていますが、＝の場合を他の場合に含めるのは間違っているのでしょうか？間違ってはいなくても、解答の正確性としては分けた方がいいのでしょうか？また、自分は学校で、場合分けの際は等号は境界の両方に付ける方が忘れなくてよいと指導されたのですが、この本では片方にのみ付けてあります。これにはどういった理由があるのでしょうか？よろしくお願いします。(2019.12.3)
A16.: ここでは、例えば $a=0$ の場合を $a\lt 0$ の場合に含めて $a\leqq 0$ としても誤りではありません。どちらがよいかとなると、それは好みだと思いますのでよいと思う方でよいと思います。ときどき、一方を頑なに主張し、譲らない人もいますが、そのような場合はそれにあわせればよいと思います。
場合分けで、等号はつねに境界の両方につける方がよいとするのは、危険です。両方につけると誤りのこともあるので、それは問題に応じて個々に考えるものだと思います。数学の問題で、「つねにこうすればよい」と言えるものは少ないと思います。
Q17.: 第５章章末問題11についての質問です。解答解説p162のように、A君がどこかの家で帽子を忘れてくる確率P(E)を余事象の確率として求めた場合、「A君がP君の家でまず帽子を忘れ、R君の家でも帽子を忘れてくる」のような場合の確率も含んでしまいそうな気がしてしまうのですが、そうはならない理由を教えていただきたいです。(2020.2.6)
A17.: これは数学の問題というよりは、解釈の問題です。これを出題した大学の原文の通り出題しましたが、P君の家で忘れた場合は、そのまま気がつかず確率1で帰宅するものとするか、帽子を忘れたまま他の家を訪問するときは確率1で気がつかないとして考えてください。
もちろんこの文章だけでそこまで読み取ることはできるのかと思う人は少なくないと思うので、原文の変更を考えています。
ここでは、この解釈でそこから先の数学の問題を考えていただければと思います。
Q18.: p.86 2.1.3 関数のグラフの平行移動についてです。「点(x,y)がC'上の点であるとは、『x軸方向に-p, y軸方向に-qだけ移動した点がC上の点になる』点である」というのは、理解した後ではなるほどと思うのですが、何かもっとダイレクトなグラフの平行移動の説明はないかと考えました。以下のように、曲線のパラメータ表示で説明するのがより自然に思うのですが、いかがでしょうか。曲線C:(x, y)=(t, f(t))を平行移動して、曲線C':(x, y)=(t+p, f(t)+q)が得られる。パラメータtを消去して、C'をグラフとする関数を求めるとy=f(x-p)+qとなる。(2020.2.24)
A18.: もちろん、そのように考えてもかまいません。曲線がパラメータ表示できる場合はその方法でできます。f(x,y)=0 のような場合は別の方法が必要になります。
Q19.: 別冊回答 p.65 下から8行目「y=xのとき最小になるから」は「y＝3のとき最小になるから」の誤植だと思います。訂正一覧に無かったのでご報告です。(2020.3.17)
A19.: 誤植のご連絡ありがとうございます。ご指摘の通りですので、訂正させいていただきます。
Q20.: 因数分解の分野についてなのですが、所謂「たすき掛け」のテクニックについての記載がありませんが、記載しない意図はありますでしょうか。(2020.4.7)
A20.: たすき掛けの方法は必要ないと判断したからです。因数分解できるものを因数分解するような場合は、そもそも有限個の組み合わせから適当なものを選ぶ作業で、運悪く他の組み合わせを調べても全数調査をすればいずれ見つかるもので、そこに早くたどり着くようになってもらいたいので、たすき掛けを経由しないでできてほしいと考えています。ただし、最初の勢いをつけるのに必要と考える人がいればそれは否定しません。私自身は教えたことはほとんどありません。
同じ意図で組み立て除法に関する記述もないはずです。
Q21.: p48 例題1について本書では有理数の定義に「mとnが互いに素である」ことを含めていませんが、例題1の解答では、有理数は互いに素な2整数の分数で表せることを前提にしています。これはつまり、「ある数を整数同士の分数で表すことができるならば、その数は互いに素な整数同士の分数で表すことができる」ことは、証明なく用いてよいということでしょうか？だとすれば、素因数分解の一意性などのように、当たり前と思えることも証明するのが数学の特徴であるように思うのですが、その違いはどこにあるのでしょうか。(2020.5.8)
A21.: まず、有理数が「互いに素である整数」の比で表されることは、p.439【互いに素の性質(5)】に書いてあります。決して当たり前のことではありません。
一方で、数学では、問われていることがどこに焦点が当たっているかを見抜くことも大切です。これは、数学だけでなく一般の質問においてもそうです。
例えば、「第2次世界大戦はなぜ起きたのか500字以内で答えよ。」という問題では、500字という制限があるので、明治維新、あるいは太古の昔から説明しては肝心なことにたどり着けません。しかし、明治のときの例えば大日本帝国憲法が全く関係ないとも言えません。ですが、与えられた枠を理解しその中に納めなくてはならないことも大切なのです。
有理数が「互いに素」である整数の比で表されることは、問題文を読んでそこにスポットが当たっていると判断できるものであれば説明します。しかし、答案のスペースや前後の流れ、あるいはもっと他に重要なことがある場合は、それを既知としてその先に重心を置くべきと考えます。
Q22.: p7の注釈4に、この結果はa<0の場合でも正しい、とありましたが、どうしてその結果がa<0の場合でも成り立つのかがわかりません。例えば|x|<=-3のとき、-a<=x<=aに当てはめると3<=x<=-3(3<=xかつx<=-3)となり成り立ちませんし、そもそも絶対値の定義から当てはまるxは存在しない(解なし)のではないかと思いました。常識はずれなことを聞いていたら申し訳ありません。どうか教えていただけませんでしょうか。(2020.6.1)
A22.: 不等式の場合は、解とは、その不等式を満たす数の集合です。$3\leqq x\leqq -3$ は、「成り立たない」のではなく、その不等式を満たす $x$ が「存在しない」が解です。集合で言えば空集合です。
一方、$|x|\leqq a (a\lt 0)$ の場合も満たす $x$ は存在しません。つまり、解の集合は空集合です。ですので、二つの不等式の解は一致するということです。
Q23.: p176第二余弦定理の証明についてですが、∠Aが鈍角の場合と鋭角の場合に分けて示されていませんが、これはθ（0°≦θ≦180°）に対して証明の過程の式が鋭角、鈍角の場合でも同じだからですか。(2020.6.9)
A23.: ここでは、座標を用いた説明なので、θが鋭角か鈍角かを分ける必要がないので分けていません。
Q24.: 86ページ C'上の任意の点を(X,Y)とおく。(X,Y)をx軸方向に-p,Y軸方向に-q とY軸方向だけ大文字となってますが誤植ですよね？(2020.7.5)
A24.: ご指摘の通り「Y軸方向」ではなく「y軸方向」の誤植です。
Q25.: 本書p482の7.1.3ですが、平行四辺形の性質に3番目の平行かつ等しいは含まれますか？含まないように思いますが。また、成立条件として定義も含める必要があると思うのですが。 (2020.7.20)
A25.: すでに四角形ができていて「1組の対辺が平行かつ長さが等しい」ことは、その四角形が平行四辺形であることと同値です。ここから平行四辺形の定義「2組の対辺が平行」は簡単に示せます。
また、「成立条件として定義も含める」の意味がよくわからないので、回答は保留させていただきます。
Q26.: ご回答ありがとうございます。類書、たとえば昇竜どうの幾何の先生、によるとプラスエリートの表記と平行四辺形の性質、平行四辺形になるための条件が明らかに違います。そのあたり、おざなりでよろしいのですか。どちらが正しいのでしょうか。まさか、多書は知らないなどと言わないでほしいです。本屋でしらべられるのですから。
何度もすみません。結局、本によっては先生のおっしゃる通り、性質に入れているものもあれば、入れていないものもある、ということなんです。ただ、条件については定義も条件に含まれるわけだから、条件にいれたらいいじゃないか、ということなのですが。先生にとってはどちらでも問題ないのですか。そのあたりの白黒をはっきりされるのが先生の流儀と思えたので。(2020.7.24)
A26.: まず、平行四辺形の性質」は代表的なものを一部選択して載せてあるだけです。幾何の性質は、ほぼどれも同じことが言えますが、「平行四辺形の性質」を「平行四辺形であれば成り立つこと」と考えることにしてこれをすべて載せることは多すぎて難しいですし、載せたところであまり意味がありません。中にはほとんど使わないものも含まれるからです。そこで、どこで線を引くかは書く人の判断になると思います。プラスエリートの場合は他書ではどこまで書いてあるかどうかは、ほとんど意識しません。意識していれば、従来の参考書ができていたと思います。さらに、どんなに有名な書籍がこのように書いてあるということであっても、一度こちらで独自に証明して吟味してから必要と判断して掲載します。この方針で、これまで検定教科書の誤りを発見してきました。このような方針ですので、ある書籍には◯◯が書いてあるのに、プラスエリートにはなぜ書いていないのだという指摘があったとしても、他の書籍が掲載している理由がわからないと答えられないこともありますし、繰り返しになりますが、どんなに権威があるという書籍に書かれてあるとしてもそれはプラスエリートに掲載するための動機にはまずなりません。大切なのは権威ではなく、内容です。
次に、「条件」というのは「平行四辺形になるための条件」のことでしょうか。まず、本書にはそのように記述はしていないので、具体的にどこを指して言っているのかがよくわかりませんでした。もしかするとp.482の「平行四辺形の性質」のことを指しているのかなと思いましたが、例えば、素数の定義として「素数は1と自分自身しか約数にもたない2以上の整数である」が書いてあったとして、次に「素数の性質」として、もう一度同じこと(「素数は 1と自分自身しか約数にもたない2以上の整数という性質をもつ」)を書くのは、書く人の判断ですが、私は避けた方がよいという考えです。
Q27.: プラスエリート 350ページ（確率分野）case2について最終行に 3/7・2/6 と二つの分数の積で求めていますが、独立ではないこのcase2で確率の積を考えていい根拠は何ページを参照すれば良いでしょうか？(2020.9.21)
A27.: あえて参照ページを言うとすれば、説明が前後していますが、p.364から始まる条件付確率の説明です。
後からかけている 2/6 は1回目に白球を取り出したもとで2回目に白球を取り出す条件付確率です。
Q28.: Q27の者です。366ページの三行目に、「一般には～」と記述がありますが、この先が成り立つ理由を知りたいです。その直前の例は分かりましたが、それが一般に成り立つ理由についてです。よろしくお願いします。(2020.9.22)
A28.: 成り立つ理由はありません。それは、それが定義だからです。$P(A\cap B)=P(A)\times \Box$ の $\Box$ に相当する部分を $P_A(B)$ (Aが起こったもとでBが起こる確率) と決めたのです。
Q29.: 約数の個数や総和問題を掲載していない理由はありますか。(2021.1.14)
A29.: プラスエリートIAには、これ以外にも一部掲載されていないものもあります。例えば、組み立て除法などもその一つです。
載せていないものには、一時的に意識することが必要かもしれないが、そのうちに使わなくなるものや、特別に説明しなくても理解できているであろうもの(例えば、偶数の和は偶数ですが、記載していません)、特にとりあげなくても、それ以降の問題で気にせず使うであろうものなどがあります。
約数の個数はほとんど自明であるのと中学入試でも現れるという考えではありましたが、気になる人が多いようであれば、改訂のときに追加しようと考えております。

プラスエリートII・B

Q1. 特性方程式について: p.664 に数列の漸化式 $a_{n+1}=pa_{n}+q$ に対して, $\alpha =p\alpha + q$ を「特性方程式」, $\alpha$ を「特性解」とありますが, これは特性方程式とは言わないのではないのではないでしょうか。
A1.: はい。原則としては言いませんが, そのように書いてある書籍もあります。プラスエリートは, 40 年以上も前からある書籍 M を参考にしてありますが, そこにはそのようにありました。また, いくつかの書籍にはある, しかし一般的な言い方ではないので, ここでは「特性方程式ということもある」という表現にしました。「いうこともある」という意味は, 少なくとも誰かが言っているということなので正しいかとは思います。この件は校正者からも指摘がありましたが, 他の「その場限りの造語」と同じ感覚で使っています。
Q2.: 直線の一般形が、y＝ax+bだと、x軸、y軸に平行な直線はなんなんですか？そして、接線問題でそのような直線が円などの接線だった場合はどうやって解くのですか？最初に断り書きを描くのですか？(2019.4.23)
A2.: この質問は、プラスエリートのどのページに対する質問でしょうか。また、具体的にどのような問題にお困りでしょうか。
Q3.: 早速ですがプラスエリートIIBのp155について質問させてください。
2^x+2^-x=tとおいて相加相乗平均によってtの動く範囲を求めるのは受験では定番かと思いますが、この部分を授業していたときに、本校の生徒で某T会に通っている者が「T会で、こういう問題は相加相乗によってtの動く範囲を出すと減点される。tの最小値が等号成立から2であるとわかっても2より大きい数をくまなくとりうるかはわからないからである。よって両辺に2^xをかけて実数解条件などでtの範囲を求めるべきだと教わった」というのです。そんな厳密な議論は入試の解答としては必要なかろうと答えましたが不安になりプラスエリートを探した結果、清先生も相加相乗平均で（あっさりと？）範囲を求めていて安心したしだいです。先生の長い受験指導暦の中で今回のような、「tの範囲を求めるために相加相乗を使うのは減点である」というような考え方を聞いたことがありますか？また、どのようなご見解をお持ちになられるでしょうか。(2019.5.29)
A3.: ご質問に対して回答させていただきます。
まず、はっきりさせておきたいのは、「t の範囲を求める」ことと「t の最小値を求める」ことは別の問題です。t の最小値を求めるだけであれば、t の範囲を求める必要はありません。「相加平均と相乗平均」の関係で得られることは t の最小値だけで、t の範囲ではありません。プラスエリートIIB の解答編の p.155 の (1) の問題は「最小値を求めよ」ですので、相加平均と相乗平均の関係であっさりと終わります。これが t の範囲を求めるのであれば、その求めた最小値からそれよりも大きい値すべてをとることを言わなければなりません。これがその問題では必要ないのであっさりとなっています。
　さて、t が 2 以上の値のすべてをとることを言うのであれば、$t=2^{x}+2^{-x}$ が x に関して連続であることを認め、x が大きくさえなればtがいくらでも大きくなることについて触れればよいと思います。本当に厳しい採点であれば、t が x について連続であることまで示せと一部の人はいうかもしれませんが、例えば $\displaystyle\lim_{x→0} 2^{x} =0$ などは指数関数が連続であることを認めているからこそ成立することで、指数関数が連続であることは普段は認めていること(ただし、証明は難しい)ですからそこを深追いはしなくてもよいと思います。
　さて、T 会の主張ですが、言っていることに間違いはありません。相加相乗平均だけでは t の最小値は求められてもそれだけでは取り得る範囲を求めたことにならないのですから。ただし、そのために 2 次方程式の解の存在条件を持ち出すといささか大がかりという印象もあります。しかし、慎重な人を非難するわけにはいかないのでそれはそれでその主張は認めなければならないと思います。
Q4.: 的外れな質問かもしれませんが、p373の下から6行目に「有理数xに対しa^x (a>0)を定義しよう．」とありますが、仮にa<0やa=0の場合を定義した場合はどうなるのでしょうか。ちょっと疑問に思って考えてみて、何か変なものになりそうですが、よくわからないので質問させていただきました。(2019.7.15)
A4.: 例えば $a=-4$ の場合 $x=\frac{1}{2}$ であれば、$x=\pm 2i$ (一つには決まらない) ということも可能ですが、$a\lt 0$ であり、$x$ が無理数の場合は、高校数学流では一般的な定義はできません。$a=0$ の場合も $x=0$ の場合は定義はせず、状況によって都合の良い解釈をすることをします。
Q5.: おそらく誤植の報告
448ページの13行目にある「x→0のとき」が「ｈ→0のとき」かと。(2019.8.11)
A5.: ご指摘ありがとうございます。
確かにご指摘通り、該当箇所は x→0 ではなく h→0です。
Q6.: p259例題2-33の解答で、「逆に円(x-3)^2+y^2=4上の任意の点は条件を満たす」と書いていないのはなぜですか。（2019.11.22）
A6.: PA>0, PB>0 であることを認めれば、その条件下ですべて同値変形をしているからです。本当は ⇔ をすべての式の前につけて変形すれば問題はありません。
教科書では、1社のものだけが、「逆も成り立つ」と記すように書かれていますが、「逆も成り立つ」を主張するのならば、その理由も書かなければならないと考えています。「逆も成り立つ」を書くと指示をされた場合は、指示をした人がどこかの変形が同値変形でないか、それが自明でないという主張です。
Q7.: p920の（１）の解答で、n個のボールがk番目の箱を除くn-1個の箱に入る確率を求めればよいことは納得したのですが、P(Ak)=(1-1/n)^nと計算できる理由が分かりません。(2020.1.24)
A7.: $n$ 個のどのボールも $k$ 番目には入らない確率を求めます。どのボールも $k$ 番目以外の箱に入る確率は, $1-\frac{1}{n}$ です。$n$ 個のボールは無作為に入れられるので、他のボールに独立に入れられると考え、$1-\frac{1}{n}$ を $n$ 個かけて $(1-\frac{1}{n})^n$ となります。
Q8.: p.70にある不等式|x+y|≦|x|+|y|を「三角不等式」と呼ぶのはどうしてですか。名前と形からすると、「三角形の成立条件」と何か関係(一方から他方が導ける、など)があるのでしょうか。それともこの二つには数学的なつながりはないのでしょうか。(2020.2.17)
A8.: 三角不等式の起源まではわかりませんが、多く言われていることは、三角形 ABC において $\rm{BC}\lt \rm{CA}+\rm{AB}$ が成り立つこと、3 辺の長さを $a$, $b$, $c$で表すとき $a\lt b+c$ が成り立ち、これをベクトルの形で表すと、$|\vec{\rm CA}+\vec{\rm AB}|\lt |\vec{\rm CA}|+|\vec{\rm AB}|$ となることから、このような不等式を三角不等式と呼ばれるようになったと考えられています。
実数 $a$, $b$, $c$ が「三角形の 3 辺の長さである」ことと、3 つの三角不等式「$a\lt b+c$ かつ $b\lt c+a$ かつ $c\lt a+b$ 」が成り立つことは同値です。
Q9.: p986~p987の(注)について2つ質問です
・p987 4行目からの“Z⊂Xでなければ”というのを“Z⊃Xならば”と置き換えても同内容でしょうか？
・g◦fが定義できてf◦gが定義出来ないような関数fと関数gの具体例を思いつけなかったので出して頂きたいです。(2020.2.25)
A9.: 最初の質問ですが、まず整理しましょう。ここでは、$f\circ g$ について考えています。$g$ は $Y$ から $Z$ への写像ですので、$g$ によってうつされた像は集合 $Z$ の要素です。これを次に $f$ でうつすのですが、$f$ は $X$ を定義域とするので、$Z$ が $X$ の中に入っていないといけないということで、$Z\subset X$ ということになっています。$Z\supset X$ では定義できませんが、$Z\supset X$ でなくても定義できない場合があるので、$Z\supset X$ が定義できないことの条件にするのはよくありません。例えば、$Z\cap X$ が空集合でも $f\circ g$ は定義できなくなります。
次の質問です。
$f$ は実数 $x$ を $x\to 2x$ によって対応させる写像、$g$ は実数 $x$ をベクトル $(x,1)$ に対応させる写像とします。この場合は、$g\circ f$ は定義できますが、$g$ の像がベクトルなので $f\circ g$ は定義できません。
Q10.: 解の変換をする理由が説明されているページを教えて下さい。自力では見つけれず質問させていただきました。(2020.4.4)
A10.: 「解の変換」とは何を指しているのでしょうか。実際にそれが行われている場面を教えていただければ回答できるかと思います。
Q11.: 102ページの116の(1) 式変形をして左辺ー右辺≦0を示して-(a-b)の二乗≦0の証明でもいいでしょうか？また受験数学において定理などの証明は理解だけでなくゼロから導出できるようになるべきでしょうか？(2020.4.18)
A11.: 最初の証明について
途中の式変形が正しければかまいません。
次の質問
一部の定理は高校の範囲内で証明することが困難なものもありますが、プラスエリートの中で証明が書かれていているものについては、導き出せるのがよいと思います。結構、厳しいですが、それが理想です。
Q12.: p.29例題1-7について次のように考えました。両辺に(x-a)(x-b)(x-c)をかけてx^2=(x-b)(x-c)A+(x-a)(x-c)B+(x-a)(x-b)C　・・・? ?の両辺にa,b,cを代入するとa^2=(a-b)(a-c)A b^2=(b-a)(b-c)B c^2=(c-a)(c-b)C A,B,Cについて整理すると A=a^2/(a-b)(a-c)　・・・? B=b^2/(b-a)(b-c)　・・・? C=c^2/(c-a)(c-b)　・・・? となる。もし与えられた恒等式が初めから?であれば、一致の定理からこの解法で問題ないと思うのですが、実際に与えられた恒等式は、x≠a,b,cについてのものです。したがって、解答の中で「x=a,b,cを代入する」ことはまずいのかな？と思いました。自分なりの精一杯考えたのは次の通りです。この解答を逆から考えていく。?かつ?かつ?のとき、?はすべてのxについて成立する。よって、?、?、?は「?が」恒等式となるようなA,B,Cである。そして?が恒等式であれば、両辺をともに(x-a)(x-b)(x-c)で割ってできたx^2/(x-a)(x-b)(x-c)=A/(x-a)+B/(x-b)+C/(x-c)も、a,b,cを除くすべての実数について、xの恒等式となる。よって?、?、?が求めるA,B,Cである。というものです。この議論の通り、与えられた式がx≠a,b,cについてのものでも、整理してからx=a,b,cを代入するのは問題ないでしょうか？(2020.4.21)
A12.: 文字化けをしているため、質問の解読ができません。文字化けをしている部分の表現を変えて再度質問してください。
Q13.: 260~261ページ例題2-34の中の、「?を?に代入した後、さらに?を変形し?に再び代入する」というプロセスがどうにも腑に落ちないというか違和感を覚えてしまうのですが、このような代入はなぜ正しいのでしょうか。些末かつ漠然とした質問ですが、お答えいただければ幸いです。(2020.4.21)
A13.: 文字化けをしているため、質問の解読ができません。文字化けをしている部分の表現を変えて再度質問してください。
Q14.: P274にてα,βが二次方程式t^2-xt+y=0の解として与えられるということですが、このようにいつも定数がある場所に変数が置かれている形の二次方程式を初めて見たためモヤモヤしています。何か不自然な気がしてならないのですが、どのように捉えれば良いのでしょうか。おんぶにだっこな質問で恐縮なのですがご教授いただければ幸いです。(2020.4.22)
A14.: $\alpha +\beta =x$, $\alpha\beta =y$ であるから、$\alpha$, $\beta$ は2次方程式 $t^2-xt+y=0$ の2解であることは、今後よく使いますので慣れていた方がよいと思います。
これは、$(t-\alpha )(t-\beta )=0$ を展開して得られます。
Q15.: P280(2)にて、α,βはt(>0)の二解であるのでα>0かつβ>0でないといけない(つまり求める条件はα+β>0かつαβ>0のみ)のではないか、と考えたのですがなぜこれは誤りなのでしょうか。(2020.4.22)
A15.: 直線 $l_{t}$ が点 $(x,y)$ を2回通る必要はないからです。$t$ は直線がいつ点 $(x,y)$ を通るときの値ですが、$\alpha \gt 0$, $\beta \lt 0$ の場合は、$t=\alpha $ のときに $(x,y)$ を通っていることになりますので、そのような点 $(x,y)$ は通過範囲としてカウントされます。
Q16.: 問2-14(1)と例題2-26(3)について質問です。x≧0,y≧0の範囲を図示してからx軸,y軸に関して折り返そうと考えました。境界はx-y=1ですがy≧0かつ0≦x<1の範囲には直線が存在しないため0≦x<1は領域に含まれないと解答しました。また、例題2-26(3)の(?)においても、y<0,x≧1の範囲には曲線が存在しないため、領域には含まれないと解答しました。なぜこれらは誤りなのでしょうか。(2020.4.26)
A16.: どちらも　(x,y の式)=0 が境界になるという発想なので、間違えてしまいます。例えば $x^2+y^2\geqq 0$ などは境界がありませんが、この不等式が表す範囲は存在して平面全体となります。
Q17.: p.955 例題9-10(2)で、問題文に「信頼度95%」が書かれていませんが、解答では信頼度95%で考えています。(1)からの流れで暗に95%で考えると誘導されるようには思いますが、(2)でも「信頼度95%の信頼区間」と断っておいたほうが良いのではないかと思いました。(2020.4.26)
A17.: これはご指摘の通りだと思います。(1) の中での「信頼度95%」なので、(2)でもそう考えるのかは、一般的には自明ではありません。
(2) の問題文の冒頭に「信頼度95%の」を入れておくように訂正表にも書いておくことにします。
Q18.: P293大問10(2)について、解答解説のP96で絶対値記号を二乗して外していますが、k≧1/3の場合とそれ以下の場合に分けて考え最終的に1/3≦k≦3/4とするのが正しいのではないでしょうか？(2020.4.29)
A18.: このままでも正しいのですが、$k\geqq \frac{1}{3}$ とそれ以外に分けてもかまいません。その場合であっても、その不等式の解は、$0\leqq k\leqq \frac{3}{4}$ になります。例えば、$k=0$ は元の不等式を満たします。
Q19.: 29ページ例題1-7について質問です。問の本題からは逸れますが(恒等式の定義に関するような質問です)、式番号(3)では「すべてのxで両辺の値は一致する」とあります。(3)から(1)に目を向けたとき、(1)⇔(2)⇔(3)かつx≠aかつx≠bかつx≠cですから、恒等式(1)の両辺は「x≠a,x≠b,x≠cで一致する」と考えてよろしいのでしょうか。(2020.5.3)
A19.: はい。それでよいと思います。
Q20.: p.1000の円と放物線が接する条件について、重解条件で得られたk=-5/4に何か図形的な意味はあるのでしょうか。円と放物線が2点で接することがない場合にこの値が一体何を表しているかが分かりません。(2020.5.5)
A20.: 実数の世界で考えている限りは特に意味はありません。
Q21.: 一次独立と一次結合の違いは何ですか？(2020.5.9)
A21.: どのあたりを見てその疑問を思いついたのでしょうか? それにそって説明します。
Q22.: P755のように、一次結合は2つのベクトルによって表すことで、一次独立はP765【2つのベクトルの1次独立の定義】によって一次結合で表されたベクトルが１つに決まるという性質で、2つのベクトル（ベクトルaとベクトルb）を司るということでしょうか？(2020.5.10)
A22.: 部分的によいと思いますが、1次結合、1次独立といった概念は、2 つのベクトルだけの話ではありません。3つのベクトル、4つのベクトルにもあります。
1次結合は、表現の問題で、与えられたベクトルを実数倍したものの和の形のことをいいます。1次独立は、ベクトル間の関係を表す用語です。
Q23.: p79 7行目あたり「となる．また，n=k+1の場合の…」とありますが、これはm=k+1の間違いではないでしょうか。(2020.5.13)
A23.: 申し訳ございません。これはご指摘の通りです。
Q24.: p.80　11行目 α^(2^m)=x_1x_2・・・x_nα^((2^m)-2) とありますが、この=は≧ではないでしょうか。(2020.5.19)
A24.: ご指摘の通り ≧ です。訂正表を更新しておきます。ありがとうございます。
Q25.: p.81　手順2による証明では等号成立条件について触れられていません。もし手順2の帰納法で等号成立条件がx_1=x_2=・・・=x_nのときであることも一緒に証明するのであれば、n=k+1のときに等号が成立する、すなわちf_(k+1)(x)=0となるときは、x=αかつ下から5行目の等号が成立するときを考えてx=α=(x_1x_2・・・x_k)^(1/k)かつx_1=x_2=・・・=x_kのときだからx_1=x_2=・・・=x_k=xのとき。よってn=k+1のときも成立。といった具合でいいのでしょうか。(2020.5.19)
A25.: ご指摘の通りです。それでよいです。訂正表を修正しておきます。ありがとうございます。
Q26.: 多項式と共通解に関する質問です。(以下登場する式はすべて多項式です)「f(x)をg(x)で割ったときの余りをr(x)とすると　f(x)=g(x)Q(x)+r(x) が成り立ちf(x)=0かつg(x)=0を満たす共通解が存在するとすれば，それはr(x)=0の解の中にある」ここまでは納得できました。しかしr(x)=0の解x=αがf(x)=0の解になっているかを確認する(十分性の議論)ときにQ(α)≠0に注意する理由が分かりません。Q(α)=0となってしまった場合，どのような不都合が生じるのでしょうか。(2020.5.23)
A26.: 具体的に、プラスエリートIIBのどこを見ての質問でしょうか。どこを見たかに応じて答えていますので、それを記していただけると答えられます。
Q27.: お忙しいと思いますが、誤植を見つけましたので報告させていただきます。P.376の一番下に書かれている極限の性質に関する注釈(6)のところですが、数列b(n)の方はlim(x→∞)ではなくて、lim(n→∞)ではないでしょうか？正否のご検討宜しくお願い致します。(2020.6.1)
A27.: ご指摘の通りです。誤植については申し訳ございません。
Q28.: 782ページ9行目から10行目にかけての式変形についてです。内積の計算なのに通常の積のように計算出来るのはなぜなのでしょうか。補足の説明は理解出来ましたので、最終的に内積の値がa1b1+a2b2となることはわかるのですが…(2020.6.24)
A28.: その部分は、p.780 の内積の性質 (1), (3) を使っています。内積の分配法則を用いて変形しています。
Q29.: P.E.数IIBにある図形と方程式の束の考え方について二点質問です、以下陰関数f(x.y)等をFと書きますm(_ _)m ?p204 注の8行目~の文章についてですこの部分は p・F+q・G=0(ただし、pもqも定数(実数)かつp^2+q^2≠0) の形でも “F=0もG=0も円の方程式であるとき、2曲線の交点を通る例えば3次関数のようなものは表せない“という解釈であってますでしょうか？ ?またこの解釈であってたとき、p199 7~10行目のP・F+Q・G=0 のようにp,qが定数でなくて多項式で(下の注釈22)を満たしていれば“F=0もG=0が円の方程式でも2曲線の交点を通る例えば3次関数のようなものも表せる”という認識は間違えでしょうか？(2020.7.5)
A29.: $p\cdot F+q\cdot G=0$ の形では、3次式になりませんから、3次関数のグラフにはなりません。
また、$P\cdot F+Q\cdot G=0$ の形でも $x^{3}$ を作ろうとすると $xy^{2}$ の項ができてしまい、この項を消そうとするとまた余分な項ができますから3次関数のグラフは無理ではないでしょうか。
Q30.: p415 注の3~4行目について質問です私はこの文章を「f＝gが成り立つとき、その両辺が正の値であるかについて、fとgは同じ値をとるので片方の辺の式が０より大きければもう一方も０より大きい事が保証されるので条件として付加するのは片方でもいい」と解釈したのですが、例えばp417の例題(2)、(3)において条件を省こうとすると答えが求まらない場合があり混乱しております。恐らく解釈が間違っているのではと思っているのですがどこが違うか見当つかないので助けて頂きたいです。(2020.8.9)
A30.: 解釈は正しいです。p.417 については、完全に $\log_{2} A =\log_{2} B$ の形になれば大丈夫です。
Q31.: p583下から五行目の「定義域内の任意の値で等しい」という部分について質問です。条件6.19の一文目に条件6.21（両辺を微分した式）が相当し、「定義域内の任意の～」という部分は条件6.19の二文目に相当すると考えたのですが、その場合「定義域内の任意の値で等しい」ではなく「定義域内で等しい値が存在する」などになるのではないのかな、と思いました。お忙しい中恐れ入りますが、簡単にでもお返事いただけると幸いです。(2020.9.27)
A31.: その通りです。$f(x)$ と $g(x)$ は定義内のどこか一つの値で等しいということです。そのどこか一つが「どこでもよい」という意味で「任意」と書いたのですが、指摘された箇所ではそのように読めずに誤解を与えることも十分に考えられますから、次の修正のときには、検討したいと思います。貴重なご指摘ありがとうございました。
Q32.: p853の注2、p850~ 例題8-30について2つ質問です。
１.vec{a}=vec{b}→vec{a}?vec{c}=vec{b}?vec{c} の逆は後件が｜vec{a}｜=｜vec{b}｜と同値なので一般に成り立たないことは分かったのですが、例題8-30 (2)の別解p853の上から8~9行目辺りで上記を用いて出た結果から解を求めることが出来たのは『３つのベクトルが一次独立より空間内で?を満たすt,u,vは唯一通りのみ存在する』という事が言えたからでしょうか？
２.それと、p854の例も見て思ったのですが一般に上記の逆を用いて解を求める事ができない時、解答の場合のように各成分を比較する方法でも解を求めることができなかったりするのでしょうか？(2021.1.6)
A32.: １．については、ご指摘の通り「3つのベクトルが一次独立であるため、t,u,vがただ一つ存在することはわかっている」というのが前提です。
２．各成分を比較する方法は有効です。ただ、成立しない場合は、t,u,vも求められない、すなわち「解なし」の状態で出てきます。
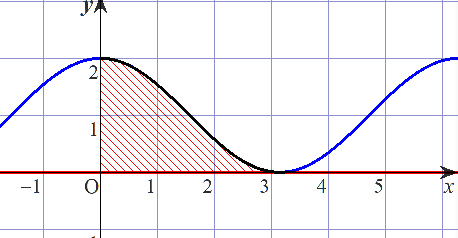
Q33.: p541の問6?10の(2)の答えがなぜπとなるのですか？(2021.1.17)
A33.: その積分が表す面積は、図の斜線部です。この $y=1$ より上の部分を切り取って、$y=1$ より下の部分の $(\frac{\pi}{2}\leqq x\leqq\pi )$にはめ込むとちょうど横の長さ $\pi$、縦の長さ 1 の長方形になり、この面積が $\pi$ となります。これが積分の値なので答は $\pi$ になります。

プラスエリートIII

Q1.

pp.315-316で、¥sum_{n=1}^{¥infty}¥frac{1}{n}=0とされていますが、これは逆数の和で、p.325で説明されている通り発散するものではないでしょうか？こちらの勘違いでしたら申し訳ありません。(2019.10.3)

A1.

誤植のご連絡ありがとうございます。ご指摘の通りですので、訂正させていただきます。訂正はここにあります。

Q2.

プラスエリート数学IIIの250ページ、問4－3の（2）についての質問です。この問題は、分子分母を2^nで割ると分子は∞に発散する項と振動する項の和になり、分母は１に収束すると思うのですが、解答では∞となっていました。∞に発散する項と振動する項の和である場合は、振動する項を無視して極限は∞とするということなのでしょうか。本文を探してみましたが、書かれていなかったと思うので、教えていただけますでしょうか。自分の見落としでしたらすみません。limn→∞｛5^n+(-3)^n/2^n+4}=limn→∞{(5/2)^n+(-3/2)^n/1+4/2^n}(2019.10.13)

A2.

ご質問の件ですが、振動する項をどんな場合でも無視できるわけではありません。この場合は、分子の ($-3)^n$ に対して $5^n$ が大きいので($n$が大きくなると十分に大きくなる)、結果影響がないということです。この部分は次のpdfファイルも参照してください。(解説pdfファイル)

Q3.

プラスエリート３の３６１ページの下から３行目のｘの範囲が、開区間になっていますが、閉区間にしなくても問題ないのでしょうか？(2020.2.1)

A3.

ご指摘ありがとうございます。これについては繊細な問題です。まず、その直前で「$x\gt 0$において $f’(x)\gt 0$」とあるので「『$x\gt 0$』において単調増加」と記述しました。(混乱しやすいからです。)
しかし、実際は $f(x)$ は $x\geqq 0$ (さらに、すべての実数) で連続で、これを認めることで、「『$x\geqq 0$』において単調増加」がいえます。現在の記述では「$x\gt 0$ において $f’(x)\gt 0$」を述べ、そのあとで $f(0)=0$ であることを述べ、そこから「$x\gt 0$ のとき $f(x)\gt 0$」を導いているので、「『$x\geqq 0$』で連続であることは認めたから」というのが、この結論が正しいことの言い訳になります。
　よりよい表現にするには、p.361 の下から 3 行目を「$f(x)$ は $x\geqq 0$ において単調に増加する」とし、欄外に「$f(x)$ は $x=0$ で連続であるから等号を入れてよい」のようにした方がよいので、このように修正します。

Q4.

プラスエリート数学IIIの、３２ページの脚注なのですが、２行目の「bは０以外の実数」は、正しくは「bは０を含む実数」ではないでしょうか。(2020.3.30)

A4.

ご連絡ありがとうございます。ご指摘の通りですので、そのように訂正させていただきます。

Q5.

いつも楽しく読ませて頂いてます。502ページの補足のところでただしadーbc≠0と書かれておりますがそれは何故でしょうか。(2020.4.30)

A5.

ad-bc=0 の場合は、ax+b が cx+d の(あるいはその逆が) 定数倍になるからです。実際に A, B の値を求めようとすると、不定あるいは不能の方程式になるので A, B は一意に定まりません。例えば、a=c=1, b=d=0 の場合を考えてみるとよいと思います。

Q6.

第３章平面上の曲線について，２次曲線等の媒介変数表示は扱われていないのでしょうか？もし別の分野あるいは書籍等で扱われている場合は該当箇所や書籍名等を教えて頂きたいです。(2020.5.14)

A6.

まず、楕円の媒介変数表示については、p.152にあります。サイクロイドやアステロイドの媒介変数表示については、入試では微分を絡めた話になるので、微分の章であつかっています。具体的には、p.413～p.446 です。
他書の話はよくわかりません。

Q7.

P660のななめ直線まわりの回転の注についてです。もちろん誤りと書いてあるだけでこれがなぜ誤りなのかわかりません。この前のページも何度も読み返したのですがわからないです。(2020.5.19)

A7.

本当の厚さは、前のページのp.659 の中ほどの図の$\Delta$OH の長さになるからです。同じ図で、点Pのx座標の増分が一定であったとしても、Pにおける曲線の接線の傾き次第で、$\Delta$OHの長さが変わります。曲線の傾きが変化するのだから、厚さも一定であるはずがないと考えてみるとよいかもしれません。

Q8.

p.661の曲線の長さの説明についてです.図の2行下の式において, 注には「平均値の定理を使って. 」とありますが, 三平方の定理ではないでしょうか.(2020.5.26)

A8.

矢印の先の式では三平方の定理を使っていますが、そこで説明していることは、矢印の指している式から、次の式の変形にあたって平均値の定理を使っているという意味です。

Q9.

プラスエリートIIIのp.743の真ん中付近「そこで，全員の体重を見てみると一番多いのはBの・・・」一番多い　→　一番大きい　or 重い（前後の文を見ると，大きいになるのかな）と思いますがいかがでしょうか．(2020.7.8)

A9.

ご指摘の通りです。「多い」ではなく「大きい」に修正させていただきます。

Q10.

p759あたりについての質問です。無限和について順序を変えてはいけないことともに収束など特別な条件のもとでは変えて良いことはわかりました。そのうえで、「部分和は有限和なので順序を変えてよい」という主張は正しいですか？私はこのように理解していたのですが、このような記述がプラスエリートをはじめ他の本でも見ないので気になりました。(2020.7.14)

A10.

部分和の中であれば、有限和なので順序を変えてもかまいません。

Q11.

こんにちわ。2次曲線の接線の方程式の証明がひとつにまとまっていると分かりやすいと思うのですが。それと陰関数の微分で出来るとありますが、できれば放物線、楕円、双曲線3つとも証明を載せて欲しかったです。結局、他の本で調べることになります。これ1冊で他は不要と謳うならば、網羅性を考えて欲しいです。できれば、他の本を本屋で参照されると比較できると思うのですが。(2020.7.26)

A11.

p.202 を見てください。

Q12.

双曲線が焦点よりも外側でありうる事はあるか？(2020.8.14)

A12.

「曲線」が「点」の外側という意味が不明なので答えられません。一般に点に内側も外側もないと思います。

Q13.

p155で三角不等式を用いてますが、もし焦点間の距離を差の一定値に考えるならば三角形はできません（Ｙ軸に対称な直線となる）僕が疑問に思うのは双曲線の定義に、『軌跡の点で焦点との三角形を作れるもの考える』のような記述がないことです(2020.8.15)

A13.

2焦点の距離を差の一定値にしたものは、双曲線の極限として考えられる図形です(直線にはなりません)が、普通は双曲線には含めません。
確かに、今のままの定義ではこれも含みますので、厳格には「2焦点を結ぶ直線以外にも通る点がある」などの追加条件が必要になります。

Q14.

p１６２での最後から二番目の行での、分母が無限大になるのはどうやって示すのですか。もしくは、trivialに扱うのでしょうか？(2020.8.16)

A14.

P162 の下から2行目には極限の式はありません。
途中の数式の最後から2行目のことであれば、分母が無限大になることは自明です。

Q15.

p.333片側極限について「aより小さい方からaに近づく場合(→)とaより大きい方からaに近づく場合(←)とでf(x)の近づく値が異なる場合は、f(x)のx→aのときの極限は存在しない」とありますが、例えばlim(x→0)(√x）のように、定義域の端で左右いずれかからは近づけることができない場合の極限はどうなりますか？左右どちらかの極限が存在しないということは少なくとも等しいとは言えないので、「極限は存在しない」という結論でいいですか？(2020.8.31)

A15.

大変よい質問です。実は、この件に関しては専門家の間でも考え方は異なるようです。すなわち、

(A): $\sqrt{x}$ は $x \geqq 0$ で定義されるのだから $ \displaystyle\lim_{x\to +0}\sqrt{x}=0 $ と書くべきで、$\displaystyle\lim_{x\to 0}\sqrt{x}$ は存在しないになる。
(B): $\displaystyle\lim_{x\to 0}\sqrt{x}$ は $\sqrt{x}$ の定義域内の $x$ に対し、0 以外の値をとり 0 に限りなく近づいたときの極限である。したがって、$\displaystyle\lim_{x\to 0}\sqrt{x} = 0$ である。

の両方があります。
　私は、$\displaystyle\lim_{x\to +0}\sqrt{x}$ の方が安全なので、人に伝えるときは、つねに「$x \to +0$」で書くことにしています。しかし、大学入試問題などでも「$\displaystyle\lim_{x\to 0}\sqrt{x}$」のように記述しているものもあり、その場合は $\displaystyle\lim_{x\to 0}\sqrt{x} = 0$ と理解して読み進めます。要するに相手に合わせるということです。
　次に、入試問題であえて「$\displaystyle\lim_{x\to 0}\sqrt{x}$ は何か」と聞かれた場合です。まず、問題が「$x \to +0$ と $x \to 0$ の違いを問う問題」であれば、出題者のセンスはなく、そういうことを問うのであれば他の例で問うべきです。つまり、そういう意味(違いを理解しているかを試す意味)では問われていないと思いますので、$\displaystyle\lim_{x\to 0}\sqrt{x} = 0$ と答えておくとよいと思います。ただし、大学入試の採点はときどき妙なものがありますから例外もあることでしょう。これが期末試験のようなものであれば、$\displaystyle\lim_{x\to 0}\sqrt{x}$ を 0 と答えても「存在しない」と答えてもどちらも正解ではないかということと、仮にばつがついたらクレームを入れられる案件かと思います。

Q16-1.

Q15の者です。ご丁寧にありがとうございます。実は一連のやりとりはツイッターで拝見させていただいていました。それを踏まえて追加で２つ質問をさせてください。
?もともとこの疑問は、連続性の定義から沸いたものです。学校の教科書では「aが定義域の左端である場合はlim(x→a+0)f(x)=f(a)が成り立つとき、f(x)はx=aで連続であるという。」とあります。（数研出版）つまり端点の場合のみ、連続性の定義自体を別物にしているのです。いただいた回答のうち、端点の極限の存在を認める立場であれば、例えば「f(x)=√xはx=0で連続か？」という問題において「f(x)は左側極限をとることができないため、lim(x→0)f(x)=lim(x→+0)f(x)=0としてよく、これとf(0)=0よりlim(x→0)f(x)=f(0)だから、f(x)はx=0において連続である」という解答で問題ないでしょうか。もしいいのなら、わざわざ端点のときだけ定義を別にしなくてもいいのですごくスッキリするのですが。(2020.9.2)

A16-1.

それでよいと思います。

Q16-2.

?そもそもx→0のときのf(x)=√xについて、ε-δ論法を考えると、「どんな正の数εに対してもx-0<ε^2を満たす定義域のxはすべて√x-0<εを満たす」が言えるから、問題なくlim(x→0)f(x)=0と言っていいのかな？と想像していました。しかし、アンケート結果があの通り割れたということは、この論法も決して完璧ではないということですか？（「定義域の」の部分かな？と思うのですがよくわからないので詳しく教えていただけたらすごく嬉しいです。）煩雑で本当に申し訳ないのですがご回答いただけたら幸いです。(2020.9.2)

A16-2.

論法が完璧でないということではなく、考える対象を定義域内にするということを前提にしておけばすむ話だと思います。アンケートの結果が割れるということは、そのあたりはあまり重要ではないということです。

Q17.

p69下から3行目 =1/2(12+6) とありますが、 =1/2(9+9) の間違いでしょうか？ 12+6で合ってるのでしょうか？よろしくお願いします。(2020.11.1)

A17.

$(3+i)(2-3i)+(3-i)(2+3i)$ をどのように計算するかだけの違いです。ですので、最終結果は一致します。{　} 内を
$(3+i)(2-3i)+(3-i)(2+3i) =(6-7i-3i^2)+(6+7i-3i^2)$
と見ると、$9+9$ になります。しかし、
$(a+b)(c+d)+(a-b)(c-d)=2ac+2bd$ と見ると
$(3+i)(2-3i)+(3-i)(2+3i) =12+6$
となります。
どちらの方法が優れているということもありませんから、$9+9$ で考えてもらってもかまいません。

Q18.

例題6-30の614ページの解説の後半に ?、?が成り立つから、dS/dθ=θ?/2である. という記述がありますが何故このようになるのでしょうか. 初歩的な質問で申し訳ありませんが、ご回答いただけますと幸いです．(2020.11.11)

A18.

$\frac{\varDelta S}{\varDelta\theta}$ の $\varDelta\theta\to 0$ とした極限が $\frac{dS}{d\theta}$ であるからです。

Q19.

解答・解説のp276の(2)の<答>の文字の右側で、xの積分が1/2 x^3となっているのですが、誤植ではないでしょうか(2020.12.26)

A19.

ご指摘ありがとうございます。ご指摘の通り誤植です。
$\frac{1}{2} x^{2}$
が正しいです。

Q20.

プラスエリート数学3の問2の10について答えはy=x^2/2√2ではないでしょうか。(2020.12.29)

A20.

ご指摘ありがとうございます。ご指摘の通りです。
正しくは、
$y=\frac{1}{2\sqrt{2}} x^{2}$ です。

プラスエリートシリーズに関する数学以外の意見・質問

Q1.

「どの本よりも深く」がコンセプトであれば、定理や性質の証明は全て記載してほしかったです。「本書ですべてを学習できるように」というのと、エリート向けという点では必要ではないかと思いました。
数学I・A
図形の性質(P480-P487)

角の二等分線の性質
多角形の内角と外角の性質
三角形の角と辺の関係
中線定理
円に内接する四角形(180度になる証明)
接弦定理
方べきの定理
中心角と円周角
円と接線(円の接線が90度になる証明)

数学II・B(P4-P6)

二項定理（数学的帰納法を使用したもの）

(2019.5.16)

A1.

貴重なご意見をありがとうございます。頂いたご意見につきましては、書籍を完成する際に検討されたものが多くあります。今回は諸事情で掲載できませんでしたが、次回に大幅改定する際にはすべては無理でもあっても、一部だけでも修正することを考えたいと思います。

Q2.

プラスエリートIIIのページ数や目次などを教えていただきたいです。(2019.6.14)

A2.

問い合わせありがとうございます。まだ発売前なので細かな情報は提供できませんが、本冊の方は本編が7章、付録がA～E という構成です。また、総ページ数は1300 前後だったと思います。

Q3.

Plus Eliteは現在全シリーズ初版のみでしょうか？高校生になる息子に、本質的な数学をさせてやりたいと買い与えたいのですが、誤植がないに越したことがないため、もし第2版以降が販売されているのならば、都内まで買いに行こうとおもうのですが...(2019.12.11)

A3.

初版の部数の関係で、数学IIBのみ初版でなく第2版が最新です。

Q4.

中学生の息子に先取り家庭学習として、高校数学を教えようとしています。プラスエリートシリーズは、そのような目的にもうってつけで素晴らしい教材だと思います。
ところでプラスエリートシリーズには、基礎的な集合論の説明に関するまとまった記述がないようで、少し意外だったのですが、これは何らかの教育的配慮によるものでしょうか。不要と判断された理由があれば、参考に教えて頂ければ幸いです。(2020.1.27)

A4.

集合論については軽視しているわけではないのですが、必要に応じて載せている感じです。例えば、数学I・A のp.247 に触れてあります。論理のド・モルガンの法則についてはp.60に、もう少し詳しいものは付録のp.578 に記述はあります。

Q5.

この春高3になった東大理一志望の受験生です。今プラスエリートIA IIB IIIを用いて勉強しているのですが、これらを一通り終わらせた後に、他に網羅系の問題集などをやる必要はありますか？それとも、もう過去問等の演習に入っても大丈夫ですか？(2020.4.11)

A5.

この本の例題と節末問題、章末問題が消化された段階で重要な問題は消化したことになります。あとは、数学 IIB・III に総合問題があるので最後にこれを解くとよいと思います。
この章だけでうすめの問題集1冊分あります。
この後は過去問の研究などをしてください。

Q6.

【不等式について】正の数の不等式の両辺の逆数をとると不等号が逆になることや複数の不等式について例えば二つの不等式の辺々を引いた後の不等式は成立するとは限らない、などの記載がありませんが、これはプラスエリートの問題の解答方針として用いない、もしくは既知である前提で書かれているからでしょうか。(2020.4.16)

A6.

書いていないのは、それ以前の話を理解していれば、そこから大掛かりな手続きを踏まなくても理解できることだからです。
例えば、(偶数)と(偶数)の和が(偶数)になることや、$\frac{1}{x}=\frac{1}{y}$ であれば $x=y$ なども書いていません。

Q7.

地方国立大学医学部志望の高2です。数学の勉強法についてわからない問題を抱えてじっくり考えるかすぐに解答を見て解答の復元の練習をするかどちらがいいでしょうか？またプラスエリートを章末まで消化したら次は過去問演習かプラスエリートの総合演習かどちらをやればいいでしょうか？(2020.4.18)

A7.

すぐに解答を見ても、きちんと身につかない方がよいので、考える時間を取った方がよいと思います。
次に、プラスエリートの章末問題までをすべて終えたのなら、総合問題に進むとよいでしょう。すべて終えれば、志望校の過去問にとりかかるとよいと思います。大学にもよりますが、過去問が易しく見えることも多いようです。

Q8.

電子書籍での販売の予定はありますでしょうか？(2020.4.22)

A8.

これは、出版社が決めることですので、出版社にお問い合わせください。

Q9.

神戸大医学部志望でプラスエリートの他に計算問題集はやったほうが良いですか？(2020.5.1)

A9.

早い段階で、「計算のエチュード」(計算の基礎・知識編) を一通り終わらせるとよいと思います。

Q10.

（本来ならば現物を書店で確認できればよいのですが、手軽の行けるほどの本屋がないくらいの田舎に住んでいるのでここで質問させてください）プラスエリートの購入を検討しています。3冊それぞれにはいくつの問題が掲載されていますか。またそれは前著の受験数学の理論と付属問題集を合わせたものよりも多いですか。よろしくお願いします。(2020.6.12)

A10.

全部数えるのはかなりの労力がいるので、おおよそでの回答をします。
受験数学の理論と問題集をお持ちの様なので、それらと比較すると、扱っている例題については、受験数学の理論に肉付けしてあるのでどの分野も減ることはありませんが、大幅に増えたということもなく、平均すると1割増くらいです。
今回は、これまでになかった「問い」をつけ(各章10～20題くらい)、節末問題(小規模の問題)と章末問題をつけています。この問題数は各章によって差があり、数学IIIの場合は、節末問題が全部で103題、章末問題は50題でした。
数学IAは厚さ的には数学IIIの7割、IIBは1割増程度です。
なお、数学IIBとIIIには総合問題があり、数学IIIの場合は重めの問題が48題あり入試数学の完成に向けて用意されています。

Q11.

私は社会人で数学の勉強のやり直しとしてこちらの検定外教科書を知りました。お聞きしたいのは検定教科書とどのような違いを意識して作られたかです。?検定教科書にあってプラスエリートにないもの ?検定教科書になくてプラスエリートにあるものなどを教えて頂ければと思います。?電子書籍の行列はどのくらい加筆されているかも教えて頂きたいです。(2020.6.17)

A11.

検定教科書は、文科省の指導要領に従うため、様々な制限を受けています。ときには、その制限が邪魔をして、学習者の発展的な考え方を妨げることもあります。
プラスエリートでは、指導要領に書かれていることは、原則としてすべて記されています。学習指導要領になくても大学入試で出題される内容もありますから、それにも対応している教科書ということになります。
電子書籍の行列は、以前「受験数学の理論」で出していたものとほぼ同じ内容です。

Q12.

先日質問させて頂いた者です。1+Aを購入し内容に大変満足いたしました。質問なのですが普段使用している通販サイト2社では2+Bと3は「メーカー問い合わせ」になっているのですが増刷しているところなのでしょうか？宜しくお願い致します。(2020.6.21)

A12.

販売に関してはこちらではわかりかねますが、現在、増刷しているという話は聞いておりません。

Q13.

プラスエリート3冊購入しました。初学なので最初は通読しようと思います。ある程度、理解したら駿台文庫の実力強化問題集を繰り返す作戦です。これで東大理系数学は5割いけますか。それとチェビシェフの多項式は扱っていますか。ないように思いましたが。(2020.7.16)

A13.

東大理系数学5割「いける」かどうかはその人次第なので判断できません。チェビシェフの多項式は扱っていません。

ご質問・ご意見のある方はこちらのページからお願いいたします。

プラスエリートに関する意見・質問

最新記事

Sep.07 2025

Sep.07 2025

Sep.07 2025

Aug.19 2025

Aug.18 2025

Aug.08 2025

Aug.08 2025

Aug.06 2025

Aug.04 2025

Jul.31 2025

Jul.31 2025

Jul.30 2025

Jul.30 2025

Jul.28 2025

Jul.28 2025

Jul.22 2025

Jul.18 2025

Jul.17 2025

Jul.16 2025

Jul.08 2025