

プラスエリートに関する意見・質問
- 数学の内容に関する意見・質問
- Q51.
- 24ページにある同値変形で「√A=√B⇔A≧0かつB≧0かつA=B」と変形しているところについて質問です。この同値変形で「√A=√B⇔A≧0かつA=B」としてはいけないのはなぜでしょうか。A≧0かつA=Bが成り立てば、必ずB≧0を満たしているように思うのですが(Bは正の実数Aと等しいため)、どこかに論理的な誤りや反例があるのでしょうか。(2021.8.26)
- A51.
- もちろん、この場合は、 \(A\geqq 0\) があれば、\(B\geqq 0\) はなくてもかまいません。
片方だけ書くと、質問が多いので両方を書きましたが、実際は片方だけの確認で十分です。 - Q52.
- p660の注:Δxだけ変化したときの厚さを√2Δxとして計算するのがもちろん誤りとありますが、なぜ誤りなのか教えて頂きたいです。また、囲まれた部分でなければ間違った数値が出てくる例を教えて下さい。よろしくお願いします。(2021.9.14)
- A52.
- 厚さは下図で書いてある部分になります。ですので、\(\sqrt{2} \varDelta x\) ではありません。
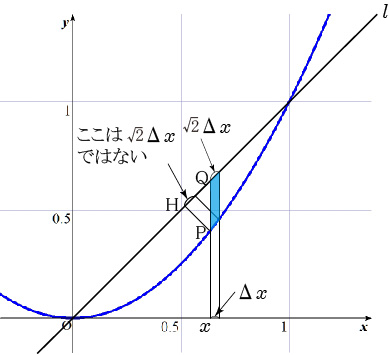
間違った例が出てくる場合は、
\(x^{2}\leqq y\leqq x\) , \(x+y\geqq \frac{3}{4}\)
を \(y=x\) のまわりに一回転したときの通過部分の体積などです。 - Q53.
- プラスエリート数学?のp.238,平面上の曲線の章末問題大問7についてです.解答では2r=√6(1-x)の両辺の2乗を計算していってますが,ここの部分の同値性は気にしなくても良いのでしょうか.(2022.1.20)
- A53.
- ここでは、r<0 の場合も含めて考えているので、気にしなくてよいのではなくて、このままになります。
- Q54.
- p279 考え方にある「方程式を解くと」の一行目は間違だていないでしょうか?(2022.2.9)
- A54.
- ご指摘ありがとうございます。おっしゃる通り、不等号は等号になります。正しくは以下の通りです。
誤:\(x^{2}\geqq x+2\) → 正:\(x^{2}=x+2\) - Q55.
- プラスエリート3の282ページの真ん中の図についての質問です。なぜan+1がanより右側に来ることがわかるのですか?(2022.3.5)
- A55.
- 理由を簡潔に言えば、\(x=a_{n}\) の付近では、曲線よりも直線の方が下側にあるからです。
図の P の座標は \((a_{n}, a_{n+1})\) です。この後、\(y=x\) 上で \(y\) 座標が \(a_{n+1}\) である点を探します。その点の座標が \((a_{n+1},a_{n+1})\) になる(これが Q)からです。そのような点は、図では P の右側にあるので、\(a_{n} \lt a_{n+1}\) となります。 - Q56.
- 私の誤解なら申し訳ないのですが、プラスエリート3の390ページにある、【第2次導関数と関数のグラフの凹凸の関係】の、「y=f(x)のグラフは下に(上に)凸」という説明で「Iで」という条件は必要ないのでしょうか。(2022.3.16)
- A56.
- これは、書き方が少し足りない部分もありました。⇒の先 (右側) は、
\(y=f(x)\) のグラフは 「\(I\) で」下に凸
が丁寧な書き方です。
「区間 \(I\) で」は、入れておいた方がよい記述で、どこでそのようなことが言えるかを表すものです。
\(y=x^{3}\) は、\(x\gt 0\) で \(y’’\gt 0\) なので、\(x\gt 0\) で下に凸ですが、「\(x\gt 0\)」がないと、実数全体では \(y’’\gt 0\) はいえないので、不都合が起こります。 - Q57.
- プラスエリート3の9ページの分数関数についての質問です。ページの最後にad-ac=0の場合は約分されてしまうとありますが、なぜ約分されるのですか。(2022.4.26)
- A57.
- \(ad-ac=0\) ではなく、\(ad-bc=0\) として答えます。\(ad-bc=0\) の場合は、\(ax+b\) の定数倍が \(cx+d\) になるからです。
例えば、\(a=kc\), \(b=kd\) とおくと、\(ad-bc=kcd-kdc=0\) になります。 - Q58.
- 30ページの章末問題の大問3についてです。領域Dの図の右側の少し線が細くなっている部分(X=14の一部)はどのように求めるのですか。(2022.4.30)
- A58.
- その部分は、式番号 6 から得られます。
中心 (6,0)、半径 8 の半円より上側の部分ですので、そのときに入る部分です。\(y\lt \sqrt{x}\) を図示するときに、\(y\) 軸の \(y\lt 0\) の部分がすべて含まれることと同じ理由です。 - Q59.
- (f??g)(x)の最小値が-1である条件において、t≦-3を除外できる理由が分かりません。y=f(t)のグラフから、「f(t)の最小値が-1」⇔「t≦-3または-1≦t」となり、tの最小値が-a^2+aであることから、t≦-3のときは-a^2+a≦t≦-3としてやれば(f(t)=)(f??g)(x)の最小値が-1になると思うのですが... Q27で同じようなことを質問されている方がいらっしゃいましたが、その回答を読んでもなお納得がいきません。g(x)が取るtの値を限定してしまうと何がいけないのでしょうか?(2022.6.4)
- A59.
- 結論を先に書きますと、\(t\) の範囲が \(t\leqq -3\) となることはなく、それは自明だからです。
\(t=x^{2} -2ax+a\) のことですから、\(t\) はいくらでも大きい値をとることができます。それは、\(x^{2}\) の係数が正だからです。ですので、\(t\) の範囲が「どこかよりも下」になることはなく、必ず 「\(t\geqq (数値)\)」となるからです。それで、\(t\geqq -1\) のみを考えます。 - Q60.
- P346のsinx/xの極限の証明についてです。この証明は教科書等にも載っているよく目にする証明ですが、以前「面積を用いた証明は循環論法に陥っている」という意見を目にしたことがあります。そのまま載せているということは、別段問題ないということでしょうか?(2022.6.6)
- A60.
- このように「どこかに何か書いてあった」系の質問はよくあるのですが、それにこたえるには、その前後も必要なので、答えることはできません。
何を議論の出発点にするかによります。p.346 に書いてある説明は、初学者向けとしては仕方ないと思います。(一部修正しました。) - Q61.
- Q60の者です。表現が拙くて申し訳ありません。単に「どこかに何か書いてあった」から質問したのではなく、それらを踏まえて「自分で具体的に論証に不安を覚える部分があるから質問している」ということです。具体的に捕捉させていただきます「円の面積が2πrになることは積分によって証明されるが、この定理自体はsinの微積を用いる。すなわちsinx/xの極限を用いる。にもかかわらず、sinx/xの極限の証明において円(実際には扇形ですが)の面積が2πrであることを用いている」のが問題ではないか?ということです。お答えいただけたら幸いです。(2022.6.7)
- A61.
- 円の面積は \(2\pi r\) ではなく、\(\pi r^{2}\) ですが、そうとらえて回答します。
「円の面積を三角関数を使う積分を用いて求め、その結果を使って \(\frac{\sin x}{x}\) の極限を求める」
というのであれば、(よく知られた)循環論法です。円の面積を小学生の方針で三角形の極限で納得させる方法も \(\frac{\sin x}{x}\) の極限を使うことになりますので、厳格には循環論法です。
ですので、本当は \(\frac{\sin x}{x}\) の極限に面積を利用することには問題はあるのですが、高校数学の説明としては私は現状のままでよいと思いますが、その点を厳格に進めたいのならば、弧長の逆関数から始めなければならないので、さらにハードルは上がります。 - Q62.
- Q59の者です。確かに2次関数であるg(x)の値域がt≧-1のようになるのは分かるのですが、そこに至るまでになぜ部分的に範囲を絞ってはいけないのか(というか、なぜそのままtのとり得る範囲に移行できるのか)が疑問でした。よく考えたのですが、xの定義域が全実数だからt=g(x)はとり得るすべての値を取れなくてはいけないからでしょうか?つまり、条件的には「"xが全実数値をとる時の"tのとり得る範囲」であるからt≦-3を排除できる。ということですか?文章が拙くて伝わっていなかったら申し訳ありません...。(2022.6.7)
- A62.
- 質問の意味がよくわかりませんでした。
「部分的に範囲を絞ってはいけないのか」
については「範囲を絞ってはいけない」という記述はなく、何のことなのかわかりませんでした。
\(t\leqq -3\) のときも、\(f(t)\) の値域は \(-1\) 以上ですが、\(t=x^{2} -2ax+a\) なので、\(t\) の範囲がそのようになることは起こりません。
必ず \(t \geqq (ある実数)\) の形をしていることは認めた上で説明しています。 - Q63.
- p292の問い4-7、(2)はどのようにして解けば良いのでしょうか?色々試しましたが上手くいきません。(2022.6.10)
- A63.
- この問いの説明については、解説動画を作りましたので、以下のリンク先を見てください。
問い4-7解説動画 - Q64.
- 337ページのしたから3行目のLimXsin1/X=0ではXsin1/Xの極限は0になるとおもうのですが極限値も0となりますか?(2022.6.11)
- A64.
- 極限が0で、これは実数の定数ですので、極限値も0になります。
- Q65.
- 数学3の問い5-5が全くわからないので解説動画を上げていただきたいです。よろしくおねがいします。(2022.6.11)
- A65.
- 解説動画を作りましたので、以下のリンク先を見てください。
問い5-5解説動画 - Q66.
- p359の対数関数の微分公式の証明のところで1/log a が微分の前後(したから3行目と2行目の間)で変化していませんがなぜですか?(2022.6.16)
- A66.
- 質問の意味がよくわからなかったので、とりあえず次の2つを回答してみます。これでも納得がいかなければ再度、言い方を変えて質問しなおしてください。
・\(\log_{e} a =\log a\) です。つまり、対数の底の \(e\) は省略できるので、下から3行目から2行目に移るときに、底を省略しています。
・\(\log a\) は定数ですので、\(\log a\) 自身を微分することはなく、単に定数倍としてかけられているだけです。 - Q67.
- p385の節末問題509について 解答例で逆を確認しているということは同値性が崩れているのだと思いますが、どのような論理関係になっているのでしょうか?微分した時点で崩れるのはわかるのですが、その後の関係がよくわかりません。(2022.6.26)
- A67.
- 結論からいえば、最終的には「多項式 \(f(x)\) が \((x-1)^{2}\) で割り切れる」ことと
「\(f(1)=f’(1)=0\)」は同値です。ですが、自明ではないと考えることもあり、ここではその説明も必要と判断して、説明をしています。
例えば、\(f(x)\) が \(f(1)=0\) を満たせば、\(f(x)=(x-1)Q(x) (Q(x) は多項式)\) となぜかけるのでしょうか? に対する説明にもなっています。
\(f(1)=0\) である場合は、多項式に限らなければ \(f(x)=e^{x} -e\) のようなものもあり、これは \(f(x)=(x-1)Q(x)\) の形ではありません。もちろん、ここでは \(f(x)\) は多項式なのでこのような関数は除外されます。しかし、本当に \(f(x)=(x-1)Q(x)\) の形で表せるのかはいろいろと知っている人は自明でしょうが、少しギャップがあるとも考えられます。\(f(x)=1+2x+3x^{2}+4x^{3}-10x^{4}\) も \(f(1)=0\) ですが、これは本当に変形すれば \(f(x)=(x-1)Q(x)\) の形になるのだろうかという疑問がある位置からの説明をしています。 - Q68.
- 大変初歩的な質問で申し訳ありません。増減表や進行表で閉区間の端点での導関数の値を書くことに少し抵抗があります。閉区間での微分可能については片側極限が存在すれば微分可能という定義だったと思うのですが実際記述する際は、端点の導関数の値を ?片側極限値として主張 ?導関数の定義域が拡張しうる 例)y’=2x(0≦x≦2)→xは任意の実数でも良い ?それ以外の主張 どのような主張で議論を進めればよろしいのでしょうか。ご教示いただけますでしょうか。(2022.6.28)
- A68.
- 閉区間 \([a,b]\) の増減表についてですが、「本当に \([a,b]\) でしか定義できない」場合と、本来は延長できるが、その場面では制限している場合があると思います。
\(y=x^{\frac{3}{2}}\) の \(x=0\) の場合であれば、\(x=0\) のときの \(y’\) は空欄にするか、\(( )\) をつけて \((0)\) くらいがよいと考えます。
この場合、\(x=0\) における微分係数については、複数の意見(存在しない・0 でかまわない)がありますので、問題の主要な話題でなければ書かないでいる方がよいと思います。
これに対して、例えば \(y=x^{4}-2x^{2}\) の増減を調べるときに、偶関数であることから \(x\geqq 0\) における増減を調べるときは、\(x=0\) のところでも \(y’\) の値は書くとよいと思います。
また、片側だけの極限で微分可能とするのは難しいと思います。\(y=|x|\) の場合を \(x\geqq 0\) に限った場合、右側極限の微分係数はありますが、このときの極限 1 が \(x=0\) における微分係数になるわけではありません。 - Q69.
- p.439のサイクロイドの面積計算の際に積分区間をx:0→2πとしていますが, x:0→2πrの誤植ではないでしょうか?そうすればθ:0→2πに対応すると思います。(2022.6.28)
- A69.
- ご指摘の通りです。
\(S=\) に続く最初の積分区間は、\(0 ~ 2\pi r\) でその右側の \(x:0\to 2\pi\) も正しくは \(x:0\to 2\pi r\) です。
訂正表に追加します。 - Q70.
- p.443 0<r<1/4 のdx/dθの符号変化についてですが -から+ではなく、+から-ではないでしょうか?(2r-1)π<-π/2であるから(1-1/2r)θが-π/2より小さい時はcos(1-1/2r)は負となるので(5.35)は負×正×負×正で、正になると思います(2022.6.29)
- A70.
- まず、\(\theta\) は \(0\) から \(2\pi r\) まで変化します。このとき、\(\cos\) の中の \((1-\frac{1}{2r})\theta (=\frac{2r-1}{2r} \theta)\) は、\(1-\frac{1}{2r}\lt 0\) なので減少し、
\((1-\frac{1}{2r})\theta\) は \(0 \to (2r-1)\pi\)
を動き、最後の \((2r-1) \pi\) は、\(-\pi \lt (2r-1)\pi \lt -\frac{\pi}{2}\) ですので、結局
\(\cos (1-\frac{1}{2r})\theta\) は+から-に変化します。\(-2(1-r)\lt 0\)、\(\sin\frac{\theta}{2r}\gt 0\) であることも考えて、\(\frac{dx}{d\theta}\) は 最初 (\(\theta =0\) 付近) では「-」、最後 (\(\theta =2\pi r\) 付近) では、「+」になります。したがって, 「-」から「+」に変化します。
なお、\(\theta\) は \(0 \to 2\pi r\) の方向に変化するので、\(\cos (1-\frac{1}{2r})\theta\) は+から-に変化することにご注意ください。 - Q71.
- p.566の区分求積法についての質問です。p.551によると区間[a,b]に対しての分割Δ={x0,x1,x2,…xn}はx0=a,xn=bであると記載されている通り,p.556の区間[a,b]に対する分割の一例は{k/n}(k=1,2,…,n}ではなく,{k/n}(k=0,1,2,…,n}ではないでしょうか?(2022.7.5)
- A71.
- ご指摘の通り \(k=0\) となります。
- Q72.
- 解答・解説p.333のルジャンドル変換についての質問があります 解説から私が理解したルジャンドル変換のイメージは y=f(x),p=f’(x)と置くとy=F(p),つまり引数をその微分に変換してf(x)の情報を等しく十分にF(p)で表せるしf(x)=F(p)(=f*(f’(x)))…(1)が成立する (1)については“g(x)=vx-x^2の最大値(v^2)/4を求めることと同じである”という解説の文から(1)が成立する.と読み取りました.ここで時刻xの時の点Pの位置yがy=x^2 と表される場合 点Pが速度vとなった時のyはv=dy/dx=2xよりx=v/2よってy=(v^2)/4と表せるし(1)よりy=f(x)=F(v)=(v^2)/4だから速度vに達した時の”位置”yはy=(v^2)/4 と理解したのですが(1)は一般に成立しないと思います.もし成立しないなら,速度vでの位置yはy=(v^2)/4にはならないかと思います. また定数aを用いてy=(x-a)^2と表せる時v=2(x-a)よりx-a=v/2従ってy=(v^2)/4となりますがルジャンドル変換の定義F(v)=f*(v)=max{vx-f(x)}(max内の変数:x)もしくはy=(x-a)^2が下に凸であることを利用してF(v)=f*(v)=f’(x(v))x(v)-f(x(v))添え字を消すとf’(x)x-f(x)(ここでxはvの式で表せることを明示するためx(v)としました)に沿ってy=(x-a)^2をルジャンドル変換するとF(v)=(v^2)/4+avとなると思います.以上から,解説内の「Pの速度がvに達したときPの位置はどこか」については,ルジャンドル変換が解決するものではないと思います.正しくは「Pの位置が時刻xでy=x^2と表される時に,同じ情報を等しく十分に説明する関数として新たにY=f*(v)=(v^2)/4を考えることができるが,このYはyではない」となると思います.なぜy=f(x)=x^2ではg(x)=vx-f(x)の最大値を求めることがPが速度vになる時の位置yを偶然表すことになってたのかつまりf(x)=max{g(x)}=f*(v)に偶然なったのかは定数aが0の場合と考えればv=dy/dx=2xよりf*(v)=f(2x)=x^2で一致してることから何かしらaが寄与してることが伺えます.実際y=(x-a)^2とするとf*(v)=f*(2(x-a))=x^2-a^2となると思います ルジャンドル変換が切片を表す事からも明らかな事実だと思います.(2022.7.31)
- A72.
- 丁寧な説明をありがとうございます。
この件については、物理の専門家とも協議しましたが、注2 については、ご指摘の通りと考え、不要な部分と判断し、削除する方向で考えています。
もう少し検討してから訂正表に載せます。 - Q73.
- 複素数平面章末問題2について、質問をお願いします。zが|z|=1を満たす全ての点を表すとき、z^nも原点中心、半径1の円周上の「すべての」点を表すと言えますか。(円周上にしか存在しえないことはドモアブルの定理から自明だとすぐわかりますが。)もし言えなければ、z=(1-+√3i)/2が?を満たすzであるという保証はないということになってしまう気がするのですが。また、一旦与えられた方程式を満たす解がz=(1-+√3i)/2であると出たにも関わらず、「その後に」nの値によって解が存在したりしなくなったりするという論理がよくわかりません。ここについて詳しく教えていただきたいです。(2022.11.25)
- A73.
- \(z\) が、\(|z|=1\) を満たすすべての点を表すとき、\(z=\cos\theta +i\sin\theta\) \((0\leqq\theta\lt 2\pi)\) と表せるので、自然数 \(n\) に対しては、
\(z^{n} =\cos n\theta +i \sin n\theta\) であるので、\(z^{n}\) は原点を中心とする半径 1 の円を \(n\) 周することになり、結果、この円上の点をすべて表すことができます。
次に、質問の内容がよくわからないところがありますが、p.43の下から2行目で得られた \(z\) は「候補」に過ぎません。
例えば、\(z^{n} =1-z\) が実現するときは、\(z^{n}, 1-z\) はともに \(\frac{1\pm\sqrt{3}i}{2}\) であるケースだけですが、このとき、同じ \(z\) になる保証はないので確認が必要です。 - Q74.
- p350(1)みたいに、分母と分子で、変数の係数が同じなら公式を利用できるという性質は、証明はどのように与えてられるのですか?(2023.1.15)
- A74.
- まず、「分母と分子で、変数の係数が同じなら公式を利用できる」という記述は、p.350 にはありません。
そこで、少し意訳して解釈することにします。
極限 \(\frac{\sin 3x}{3x}\) のような場合に、分母の \(x\) の係数 3 と、分子の \(x\) の係数 3 は一致しています。ここでは、\(x\) の係数が一致しているだけならば、\(\frac{\sin (3x+1)}{3x}\) の場合も含まれてしまうので、公式 (たぶん \(\displaystyle\lim_{x\to 0}\frac{\sin x}{x} =1\) のことを指している?) は利用できません。
横の欄外には、\(\frac{\sin △}{△}\to 1\) が書かれていますが、これは、三角の部分が完全に一致している場合の話です。これの証明は、p.346 から始まる \(\displaystyle\lim_{x\to 0} \frac{\sin x}{x} =1\) の公式の証明そのものですので、こちらで示されています。 - Q75.
- Q74を質問した者です。こちらの質問の記述が悪かったので再び質問させてもらいます。「三角部分」が共通してると、公式を利用できますが、その証明が気になったという事です。sinx/xの極限公式からは、この事は自明に導けるとは思わないからです。(2023.1.15)
- A75.
- \(\displaystyle\lim_{x\to 0}\frac{\sin x}{x} =1\) の意味するところは、「\(\frac{\sin △}{△}\) の形の式が △ の部分が 0 に限りなく近づけば、その値が 1 に限りなく近づく」ことを表したものです。\(\frac{\sin x}{x} \to 1\) の \(x\) の部分は、\(x\) が 0 に近づくのであれば、 \(x\) である必要はありません。
\(\frac{\sin x^{2}}{x^{2}}\to 0 (x\to 0)\) であったり、\(\frac{\sin e^{-x}}{e^{-x}} \to 1 (x\to \infty)\) もこの一つの式からいえます。
これは、\((x+y)^{2}=x^{2}+2xy+y^{2}\) を学習したときに、文字は \(x, y\) に限らなくてもよいというのと同じです。この展開公式を学習したときに、\((a+b)^{2} =a^{2}+2ab+b^{2}\) をも学習したことになることと同じです。 - Q76.
- 解答のp5でtのとり得る範囲がt≦-3となるのはなぜですか?(2023.1.23)
- A76.
- p.5 には「\(t\) のとり得る範囲が \(t\leqq -3\) であることはない」と書かれていますので、質問の意図を「\(t\leqq -3\) とならないのはなぜか」という意味だと解釈して回答します。もし違っていたら再度質問してください。
同様の質問が過去にありますので、Q27に対する回答を参照してください。 - Q77.
- p18の「一般に、y=f(x)で表される曲線と、xとyを入れ換えたx=f(y)で表される曲線は直線y=xに関し対象になる」という理由が分かりませんでした。(2023.1.26)
- A77.
- まず、点 \((a,b)\) と点 \((b,a)\) は直線 \(y=x\) に関し対称です。
次に、曲線 \(y=f(x)\) が点 \((a,b)\) を通るとします。これは、\(b=f(a)\) が成り立つことになります。すると、曲線 \(x=f(y)\) は、\((x,y)=(b,a)\) のとき \(x=f(y)\) を満たすので、\(x=f(y)\) は点 \((b,a)\) を通ります。
以上から、曲線 \(y=f(x)\) が通る点を直線 \(y=x\) に関して対称に移動した点をすべて曲線 \(x=f(y)\) が通る(逆もいえる)ので、\(y=f(x)\) と \(x=f(y)\) は \(y=x\) に関して対称であるということになります。 - Q78.
- 解答p25の(3)のcos(-10分のパイ)をcos10分のパイとしてはダメですか?(2023.2.18)
- A78.
- 極形式は、 \(r(\cos\theta +i\sin\theta )\) ですので、\(\theta\) には同じ角が入ります。また、\(r(\cos\theta -i\sin\theta )\) のように \(\sin\theta\) の係数が \(-i\) になってもいけません。
\(\cos (-\frac{\pi}{10}) =\cos(\frac{\pi}{10})\) ですが、そのとき、\(\sin(-\frac{\pi}{10})=-\sin(\frac{\pi}{10})\) になるので、極形式にならないため、ここではよくありません。 - Q79.
- p98の別解にあるz=i分のωの式についてこれはωを-2分のπだけ回転した点とありますが、iを極形式で表すと<1,2分の3π>分数の分母にiがあるので、ωの偏角をθとでもするとi分のωの偏角はθ-2分の3π,すなわち-2分の3π+2nπから-2分の3π=2分のπとなって2分のπだけ回転するのではないかと考えました。初歩的な質問ですがよろしくお願いします。(2023.2.28)
- A79.
- \(i=\lt 1,\frac{3}{2}\pi\gt\) ではなく、\(i=\lt 1, \frac{\pi}{2}\gt\) です。ですので, \(\frac{\omega}{i}\) の偏角は、\(\theta - \frac{\pi}{2}\) になります。
- Q80.
- プラスエリート数学?p388の下2行、論理的に誤りではないですか?まず、定理にはIが閉区間か開区間かに言及していない為に、p388の証明の下2行の所でIを閉区間とおいてます。ここでIにおいて導関数の符号が正という定理の仮定を持ち出してますが閉区間の端点では微分係数が定義できないので、閉区間で導関数が正であるというのは変です。1番下の行でも開区間で微分可能であると書いてあるので整合しません。確かに微分可能な開区間では連続ですが、開区間で微分可能であるならばその端点を含む閉区間で連続であるという定理も聞いた事がありません。是非とも解説をお願いします。(2023.3.9)
- A80.
- 貴重なご指摘ありがとうございます。すみません。そこは誤植でした。
p.388 下から2 行目
(誤) \(I=[a,b]\) (正) \(J=[x_{1}, x_{2}]\) です。
そのあとの「\(f(x)\) は \(I\) において \(f’(x)\gt 0\) であるのだから」はそのままで、そのあとは
(誤) もちろん \(I\) で連続で, \((a,b)\) で微分可能である (正) もちろん \(J\) で連続で, \((x_{1},x_{2})\) で微分可能である
このようになります。
なお、【定理】の中の \(I\) が閉区間で、\(J=I\) の場合ですが、例えば、
「関数 \(y=x^{2} (x\geqq 0)\) は \(x=0\) で微分可能か?」
については、数人の数学者にも確認しましたが、「微分可能」とすることの方が多いようです。 - Q81.
- プラスエリート? p.617 ΔVを近似する の説明の中の |S'(k)|≦M が何を表してるのかがわかりません。よろしくお願いします(Mは最大値ですか?何の最大値かもわからないので教えていただけると嬉しいです)(2023.3.11)
- A81.
- その \(M\) は「さらに、\(|S’(k)|\leqq M\) であるとする」で定めたものです。もう少し詳しく説明します。
\(S’(k)\) の仮定として、\(|S’(k)|\) が有界、つまり、どこまでも大きくなることはないというものとします。
したがって、どこまでも大きくならないので、大きな値には限界があって、「すべての \(|S’(k)|\) の値は、この値よりは小さい」の「この値」が選べます。それを \(M\) としました。\(M\) のとり方は一通りではありません。
例えば、\(S’(k) =\sin k\) は有界ですが、すべての \(k\) に対して、\(|S’(k)|\lt 2\) が成り立ちます。この 2 は 3 でもかまいません。
つまり、すべての \(k\) で \(|S’(k)|\lt M\) となる \(M\) が存在します。
「さらに \(|S’(k)|\leqq M\) であるとする」
の部分は
「さらに、\(|S’(k)|\) は有界であるとする。有界なのである値を超えられないので、その値を \(M\) とする。」
のように読んでください。 - Q82.
- p130例題3-3について質問です。解答5行目の4p1k=4p2すなわちp1k=p2の方程式の左辺はkが0より大きい実数であるからこの方程式を満たすようなkは存在する。したがってc1を適当に拡大するとc2に一致させることができる。これだと証明できてませんかね?(2023.3.16)
- A82.
- この場合は、\(k\) の存在がいえればよいので、いただいた説明でもかまいません。ここでは、\(k\) が求まるので求めてしまえば存在もいえるということでこのように書いてあります。
- Q83.
- P.17 節末問題104(2)に関する質問です.平行移動して重ね合わせることができる条件がなぜ解説のようになるのかがわかりません.y=(k/x-p)+qの式のkの部分が一致すれば平行移動して一致すると書かれていますが,丸1番の式のk部分の値は1なので,自分はc-8=1になるのでは?と考えました。どうしてc-8=1/2になるのかを教えて欲しいです.(2023.3.25)
- A83.
- 解答の中の ① は,
\(\displaystyle y=\frac{1}{\boldsymbol{2}\left(x+\frac{1}{2}\right)}+2\)
ですが, これは,
\(\displaystyle y=\frac{\boldsymbol{\frac{1}{2}}}{x+\frac{1}{2}}+2\)
のことなので, (2) の解答の中の
\(\displaystyle y=\frac{\boldsymbol{c-8}}{x+4}+2\)
と比較するときは,
\(c-8=\frac{1}{2}\)
となります。 - Q84.
- 質問です。6ページの問い1-2 (3)の途中式を教えて欲しいです。自分でも計算してみましたが、xについてどのように解けばいいかわかりません(2023.3.29)
- A84.
- 次のようになります。
【問い 1 ー 2 】(3)
\(y=x^{2}+2x\) とおく。
\(x^{2}+2x-y=0\)
を \(x\) について解いて,
\(x=-1\pm \sqrt{1+y}\)
このうち, \(x=-1-\sqrt{1+y}\) は \(x\geqq 0\) を満たさない。
また, \(x\geqq 0\) のとき \(y\geqq 0\) をとるから,
\(x=-1+\sqrt{1+y}\) \((y\geqq 0)\)
したがって,
\(f^{-1}(x)=-1+\sqrt{1+x}\) \((x\geqq 0)\)
である。 - Q85.
- p175y^2=4px(p≠0)...(A)上の(x0,y0)を通る接線についてですが、y=m(xーx0)+y0,(m≠0)...(B)としてこれを(A)に代入したときに現れるxの式の判別式D=0をmについて解いた値を代入した直線というのは、放物線の原点以外の点(x0,y0)における接線を表せるのでしょうか。読みづらい文で恐縮ですがよろしくお願いします。(2023.4.6)
- A85.
- 表せます。ですので、その方針で原点以外の接線を求めるという方法もあります。
- Q86.
- p187例題3-10についてですが、P(x1.y1).Q(x2.y2)としたときに、QRの式を本書と同じような方針かつ、楕円の接戦の式を用いないで求めることは可能でしょうか。傾きを使った直線の方程式に同じように代入する方法でやってみたのですが、煩雑になってしまってよく分かりませんでした。(2023.4.15)
- A86.
- 「P(x1.y1).Q(x2.y2)としたときに」の部分は「\({\rm Q}(x_{1}, y_{1}), {\rm R}(x_{2}, y_{2})\) としたときに」と解釈しました。
その上で、質問の内容がよくわかりませんでした。
「QRの式を本書と同じような方針かつ、楕円の接戦(接線と解釈しました)の式を用いないで」
の部分ですが、「本書と同じような方針」では、楕円の接線の方程式は用いています。ですので、「本書と同じような方針」かつ「楕円の接線の式を用いない」の意味が通じませんでした。
もしも、直線 QR の傾きを求めてから、直線 QR の方程式を求めようということならば、一度円に変換するなどの工夫をしないと、大変な計算になります。原理的に不可能ではありませんが。 - Q87.
- 573ページの例題ですが、f(x)がx^(1/2) ではなくx^2になる理由が理解できません。どうしてこのような式変形をするのかお教え願えないでしょうか。(2023.5.20)
- A87.
- ここでは、区間 \([0,1]\) を \(\sqrt{\frac{k}{n}}\) で分割しているので、\(x=\sqrt{\frac{k}{n}}\)、\(y=\frac{k}{n}\) と見て、面積を考えています。
すなわち、\(\sum\) 内の \(\frac{k}{n}\) は長方形の縦の長さ、\(\sqrt{\frac{k}{n}} -\sqrt{\frac{k-1}{n}}\) は長方形の横の長さと考えています。
ですので、\(y\) を \(x\) で表すと、\(y=x^{2}\) の関係がありますから、\(y=x^{2}\) の面積を考えています。 - Q88.
- Q87で質問した者です。こんなにも早くお答えをいただき感謝しております。その間に考えたのですが、573ページの例題は、k=1からnまで書き下して最終的に、1ー(1/n)Σ(k/n)として区分求積法のその他の例題と同様の解き方をしたのですが、この解き方でも良いのでしょうか。最終的な答えは1/3となりました。(2023.5.20)
- A88.
- その考え方でも大丈夫です。
- Q89.
- p530問い6-14(2)で例題6-15で示したものを利用して式変形すると、\int_{0}^{\pi} x\sin^{3}(x) dx が得られますが、これ以降の計算過程を教えてください。よろしくお願いします。(2023.6.5)
- A89.
- 【問い 6 - 14 (2) の計算】
定積分 \(\displaystyle \int_{0}^{\pi}x\sin^{3}x\,dx\) の計算は次のようになる。
3 倍角の公式 \(\sin 3x=3\sin x-4\sin^{3}x\) より、
\(\displaystyle \sin^{3}x =\frac{3}{4}\sin x-\frac{1}{4}\sin 3x\)
であることを用いると、
\(\displaystyle \int_{0}^{\pi}x\sin^{3}x\,dx=\int_{0}^{\pi}x\left( \frac{3}{4}\sin x-\frac{1}{4}\sin 3x\right)\,dx\)
\(\displaystyle =\frac{1}{4}\int_{0}^{\pi} (3x\sin x-x\sin 3x)\,dx\)
\(\displaystyle =\frac{1}{4} \left[ 3(-x\cos x+\sin x)-\left( -\frac{1}{3}x\cos 3x +\frac{1}{9}\sin 3x\right) \right]_{0}^{\pi}\)
\(\displaystyle =\frac{1}{4}\left( 3\pi -\frac{1}{3}\pi\right)\)
\(\displaystyle =\frac{1}{4}\cdot \frac{8}{3}\pi\)
\(\displaystyle =\frac{2}{3}\pi\)
(注) \(x\sin x\), \(x\sin 3x\) の積分は、p.540 以降の方法を用いたが、コツコツ部分積分を行なってもよい。 - Q90.
- プラスエリート3のp592の(617)において不等式e^{x} \geqq 1+x を用いて評価していますが、この不等式が思いつきません。(解答を見てなんとなくの理解はしました。) どのような発想をしたのでしょうか。アドバイスよろしくお願いします。(2023.6.15)
- A90.
- 確かに、\(e^{x}\) を \(1+x\) で評価する発想は初めての人には難しいと思います。
関数の評価は、調べたい点のまわりの接線で比較することが多くあります。この場合も \(y=e^{x}\) の \(x=0\) における接線を利用しています。
\(y=e^{x}\) のグラフは下に凸なので、接線 \(y=1+x\) はグラフより(接点を除けば)下側になることを利用します。
一度、このようなものを見た後は、これは定番の評価方法なので知っておくとよいでしょう。 - Q91.
- 解答編116ページの(4)についての質問です。解説の中ほどに N=3mのとき~ とありますが、何故、Nを3で割ったあまりで分類することを思いつくのでしょうか。大変お忙しいと思いますがよろしくお願いします。(2023.8.4)
- A91.
- \(\displaystyle a_{n} =\left( \frac{1}{2}\right)^{n}\sin \frac{n\pi}{3}\) は、\(\displaystyle \sin \frac{(n + 3)\pi}{3} = − \sin \frac{n\pi}{3}\) であることから、
\(\displaystyle a_{n+3} = − \frac{1}{8} a_{n}\)
という性質をもっています。すなわち、どの項も 3 つ先は \(− \frac{1}{8}\) 倍された値になります。
このことから、\(a_{1} + a_{2} + a_{3} + a_{4} + \cdots\) は、
\((a_{1} + a_{2} + a_{3}) + (a_{4} + a_{5} + a_{6}) + (a_{7} + a_{8} + a_{9}) + \cdots\)
のように 3 つずつまとめて加えていくと和が求めやすくなります。この場合は、
\(\displaystyle (a_{1} + a_{2} + a_{3}) + (a_{1} + a_{2} + a_{3}) \cdot \left(− \frac{1}{8}\right)+ (a_{1} + a_{2} + a_{3})\left(− \frac{1}{8}\right)^{2}+ \cdots\)
のようになります。
この和の最後の項ですが、3 つずつまとめるので、最終項を \(a_{N}\) とすると、\(N\) が 3 の倍数のときが数えやすいのでまず、\(N = 3m\) の場合から考えます。\(N = 3m + 1\)、\(N = 3m + 2\) のときは、最後に「余った項」が出るので少しの手直しが必要になるので \(N = 3m\) の場合と分けて考えることになります。 - Q92.
- P661最終行「右辺の和の極限は定積分...に収束すると考えて」とありますが、なぜそのように考えられるのかがわかりません。解説していただけると助かります。(2023.11.20)
- A92.
- この部分はあっさりと書いていますが、その理由はそれ以前に扱った考え方を使っているからです。それは代表値と増分をかけたものの和の極限が積分で表されるというものです。区分求積法などでもこの考え方は使っています。もう少し細かい説明としては、p.913 の D.9 の「積分の考え」も参照してください。
- Q93.
- p347の¥lim_{x→-0} ¥frac{¥sin x}{x}の証明において、f(x)=¥frac{¥sin x}{x}とおき、f(x)が偶関数 かつ ¥lim_{x→+0} f(x)=1であるから、¥lim_{x→-0} f(x)=1さらに、¥lim_{x→0} f(x)=1と考えてみたのですが、このやり方は数学的に大丈夫でしょうか?(2024.4.13)
- A93.
- \(f(x)\) は偶関数ですので、\(x=-t\) とおけば
\(\displaystyle\lim_{x→-0}f(x)=\lim_{t→+0}f(-t)=\lim_{t→+0}f(t)=1\)
となるので、その説明で大丈夫です。 - Q94.
- p560 定積分の平均値の定理について この定理は検定用教科書では公理として(証明なく当然成り立つものとして)、面積を微分するともとの関数になることの証明に用いられています。しかしそれでは曖昧さが残るため、プラスエリートではさらにその前段階の最大値の定理も含め、丁寧に証明が掲載されているのだと思います。その観点で読み進めていったとき、少し疑問に思う点があります。このp560の下から2行目の不等式は当然成り立つと言ってしまっていいのか、ということです。それを当たり前といっていいのであれば、そもそも検定教科書の立場と同じく、定積分の平均値の定理自体も、そもそも当たり前と言ってしまってもいいのでは?と思ってしまいます。それを踏まえて2点質問させてください。 質問1. 「最大値Mと最小値mに対してp560下から2行目の不等式が成立する」ということは数学家の間では証明なく用いてよい事実ですか?もしくは実際にはきちんとした証明があるものの、ここでは省略しているだけですか? 質問2. もし質問1に対する解答が前者であったとするならば、証明すべきことと証明せずに用いていいことを、数学家はどこで判断しているのですか?個人的には「定積分の平均値の定理や最大値の定理は証明なく用いてはまずい」にもかかわらず「p560下から2行目の不等式は証明なく用いてよい」という線引きには違和感があります。(2025.1.29)
- A94.
- まず、私の認識では、p.560 にあるような「定積分の平均値の定理」は文科省検定教科書には書かれていないと思いましたが、すべてを調べたわけではないので断言はできません。ということで、まずそこが引っかかりました。ただ、「面積を微分すると元の関数になる」とも書かれているので、もしかして「微積分学の基本定理」のことかなとも思いましたが、その後で「最大値の定理」の記述があるのでそれも違うと思い、結局、こちらとしては、質問の意図が正確にとらえていない可能性がありますが、できるかぎり回答させていただきます。
質問1. について、「p.560 の下から2行目の式」ですが、数学的には公理ではありません。ただ、p.556 にあるリーマン和の話からの流れからすればほとんど自明なことではあると思います。ですので、話題がその式の証明などにない限りは毎回証明などはしませんが(それは明らかなので)、例えば大学入試などでは説明なく用いてよいものと考えます。(正確には入試の採点者に聞かないとわかりません。)
質問2.の、「証明すべきこと」と「証明せずに用いてよいこと」の境界は、その時点でその事実がどのくらい話の根幹に関わってくるかによって判断します。その判断力はついていないといけないと思います。判断できるためには、一つの話をするときにその事実の証明などにおける役割を理解している必要があります。「最大値の定理」にも、何を伝えようとしているかによって、「証明は今は不要」というときと、(話の根幹に関わるので)「証明は必要」というケースがあります。
プラスエリートIII
Q1. ~ Q50.
最新記事
Feb.03 2026
第14回教育課程企画特別部会について
2月2日に文科省で開催された…
Jan.23 2026
第5回算数・数学ワーキンググループについて
1月23日に文科省で開催され…
Jan.05 2026
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で『5 …
Jan.04 2026
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で『1 …
Jan.03 2026
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で『1 …
Dec.28 2025
「数学ラウンジ」動画公開のお知らせ
YouTube 数学ラウンジ…
Dec.25 2025
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で『10…
Dec.23 2025
第4回算数・数学ワーキンググループについて
12月22日に文科省で開催さ…
Dec.17 2025
新刊のお知らせ
新シリーズ「数学の受験教科書…
Dec.15 2025
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で数学の…
Dec.13 2025
第3回算数・数学ワーキンググループについて
12月12日に文科省で開催さ…
Dec.01 2025
新刊のお知らせ
新シリーズ「数学の受験教科書…
Nov.25 2025
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で数学の…
Nov.22 2025
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で『8 …
Nov.15 2025
第2回算数・数学ワーキンググループについて
11月14日に文科省で開催さ…
Nov.09 2025
「エチュードクラブ」ページ更新のお知らせ
「エチュードクラブ」で戦略編…
Oct.19 2025
第1回算数・数学ワーキンググループについて
10月17日に文科省で開催さ…
Oct.12 2025
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で数学の…
Oct.07 2025
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で『6 …
Oct.05 2025
「受験教科書クラブ」ページ更新のお知らせ
「受験教科書クラブ」で数学の…





